Inscription / Connexion Nouveau Sujet
Densité d'états en énergie pour des rotons
Bonjour !
Je rencontre un petit problème sur un exo de physique statistique, j'espère que quelqu'un pourra m'aider.
Il s'agit d'étudier la phase superfluide de l'hélium 4, qui apparaît pour des températures inférieures à 2,17 K. Dans une première partie, on étudie l'hélium en supposant qu'il s'agit d'un gaz parfaits de bosons, et on montre que ce modèle n'est pas satisfaisant, puisqu'il n'est pas en accord avec l'expérience, qui indique que la capacité calorifique varie en en-dessous de 0,6 K.
On essaie alors de traiter le problème en considérant les interactions entre les atomes. Pour simplifier, on remplace l'étude du gaz de bosons par l'étude de quasi-particules indépendantes, correspondant aux excitations du gaz (comme on le fait dans un solide avec les phonons). Ces quasi-particules sont des bosons de spin nul, et leur énergie suit la relation de dispersion donnée sur la figure ci-dessous :
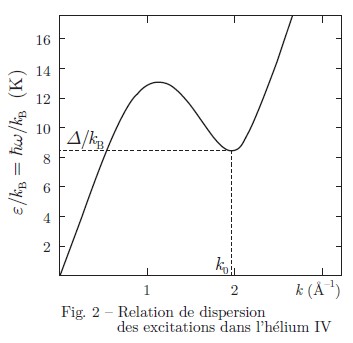
L'énoncé indique que deux zones sont remarquables et vont contribuer à basse température :
1. La partie linéaire rappelle les phonons, avec une relation de dispersion .
2. La courbe présente un minimum en ,
, avec
. Les excitations autour de ce minimum s'appellent les rotons, et leur énergie obéit à la relation :
où ,
étant naturellement la masse d'un atome d'hélium 4.
On me demande dans un premier temps d'écrire la densité d'états et le nombre moyen d'occupation
d'un état d'énergie
. Il s'agit de quelque chose d'assez habituel (à moins qu'une subtilité ne m'échappe), donc on doit avoir :
et :
Ensuite, on traite le cas à très basse température, en considérant que seuls les phonons contribuent à l'énergie (et donc à la capacité calorifique). Pas de problème, je le fais et retombe sur la loi en observée expérimentalement pour la capacité calorifique.
Là où ça coince, c'est pour la suite. On me demande déjà de justifier pourquoi, en augmentant un peu la température (jusqu'à 1 K, environ), ce sont les rotons qui contribuent majoritairement à l'énergie, alors que leur énergie est bien plus grande que l'excitation thermique. Je ne suis pas tout à fait sûr de moi, mais j'imagine qu'à cette température, pour les quasi-particules considérées, la distribution de Bose-Einstein tend vers la distribution de Maxwell-Boltzmann. Tous les états sont donc très faiblement peuplés, mais la densité d'états est sûrement bien plus grande pour les rotons que pour les phonons, ce qui explique qu'ils soient présent en plus grand nombre.
Malheureusement, ça se gâte dans la suite. Je dois calculer le nombre de rotons à 1 K, mais je n'y parviens pas. Comme pour les phonons (calcul à très basse température), je calcule d'abord la densité d'état . On doit avoir :
puisque la relation de dispersion est isotrope. Le nombre de rotons est alors :
Malheureusement, la courbe présente un minimum en
, soit une annulation de la dérivée en ce point, qui implique une densité d'états
... infinie. Il va de soi que ça me paraît difficilement concevable physiquement (quoi que ça correspond à un continuum d'énergie, je suppose), mais, surtout, ça fait dangereusement diverger l'intégrale que je veux calculer !
Je n'arrive vraiment pas à mettre le doigt sur ce qui ne va pas. Si quelqu'un pouvait m'aider, ce serait grandement apprécié ! 
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()


