Inscription / Connexion Nouveau Sujet
Condensateur
Bonsoir
Pouvez vous m'aidez avec cet exercice ..
La moitié de l'espace entre deux armatures d'un condensateur sphérique est remplie d'un diélectrique homogène isotrope de permittivité 'epsilon'. La charge du condensateur est q . Déterminer le module du vecteur intensité du champ électrique entre les armatures en fonction de la distance r au centre de courbure de ces armatures .
Bonsoir
Ta description est très imprecise. Je note R1 Le rayon de l'armature interne et R2 le rayon de l'armature externe et d la différence (R2-R1). Faut-il comprendre que l' isolant occupe l'espace entre les sphères de rayons R1 et (R1+d/2), l'espace entre les sphères de rayons (R1+d/2) et R2 étant vide? Si oui, il suffit d'appliquer le théorème de Gauss.
Merci pour votre réponse. .
L'espace entre les deux armatures (R1 et R1 ) est divisée à deux .. la moitié est réservé pour le diélectrique , l'autre est le vide .. j'espère que j' arrive à bien expliqué .
Merci pour votre réponse. .
L'espace entre les deux armatures (R1 et R2 ) est divisée à deux .. la moitié est réservé pour le diélectrique , l'autre est le vide .. j'espère que j' arrive à bien expliqué .
j'espère que j' arrive à bien expliqué .
Pas vraiment! S'il s'agit de la répartition moitié moitié que je t'ai décrite, Le centre des sphères est centre de symétrie et le théorème de Gauss s'applique. Si l'isolant occupe la totalité de l'espace entre les sphères d'une moitié de condensateur le théorème de Gauss ne s'applique pas.
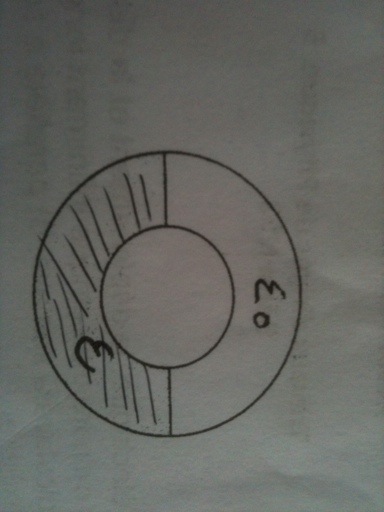
Es-tu bien sûr de ton schéma ? Est-ce une reproduction à main levée de celui fourni par l'énoncé ou est-ce ton interprétation personnelle de la notion de "moitié" ?
Mon interprétation donnée hier à 20h31 permet une étude rigoureuse à l'aide du théorème de Gauss. Si la tienne est bien celle à étudier, il n'existe pas de solution rigoureuse à ton problème ! Tout au plus, peut-on fournir une solution approchée valide seulement dans la mesure où d<<R1 ...
Cela dit, je suis presque sûr d'avoir raison. Sinon, on demanderait deux expressions différentes de E en fonction de r, selon la moitié concernée...
Oui je suis sûre du schéma il est donnée avec l'ennoncé .. si on chercher 2 expressions du champ E selon la moitié concernée , on applique théorème de gauss généralisé deux fois avec l'integrale double D.ds=Qlibre/2 ou l'integrale double D.dS=Qlibre
En toute rigueur, on ne peut pas appliquer le théorème de Gauss à une sphère de rayon r et de centre O (le centre du condensateur sphérique) ! Avec ton schéma, ce centre O n'est pas centre de symétrie car la charge q dont parle l'énoncé ne se répartit pas uniformément sur l'armature sphérique mais cela ne semble pas gêner le concepteur de cet énoncé ! Je voudrais bien savoir dans quel cadre cet énoncé est posé et quelle est la compétence de celui qui le pose !
Il était donné dans un examen et j'ai trouvé que son corrigé n'est pas logique , ils ont appliquer le théorème de gauss ..
La solution est donnée de cette manière : D (1) pour milieu diélectrique et D(2) pour mileu vide
D.dS = q = D(1).S/2+ D (2).S/2 = 
E(1).S/2 + 0.E(2).S/2 et ils ont supposé que E = E (1) = E (2) pour le plan de separation ce qui donne : E =q/(2
0.r.(1+(r)))
est-ce que c'est juste ? 
Bonjour
est-ce que c'est juste ?
La formule que tu as écrite est-elle bien celle-ci ?
Si oui : ce résultat est évidement faux ! Cela apparaît sans chercher à résoudre le problème, rien que par l'analyse dimensionnelle !
1° L'écriture
dépend de r. Cela ne cadre pas avec ta description du condensateur. De plus et plus grave : a la dimension d'une capacité divisée par une longueur ; elle se mesure en F/m : impossible d'ajouter un simple nombre ("1") à une telle grandeur.
2° Il s'agit peut-être d'une simple maladresse d'écriture ; il faut peut-être comprendre :
où
r est la permittivité relative de l'isolant, grandeur sans dimension que l'on peut ajouter à 1. Un autre problème se pose alors ; tu connais sûrement l'expression de l'intensité du vecteur champ créé par une charge ponctuelle qo à la distance r dans le vide :
Dans l'expression de E, r doit apparaître au dénominateur à la puissance 2 ; or la permittivité relative est strictement supérieure à 1 !
De toutes façons, le centre O n'étant pas centre de symétrie pour le condensateur, le théorème de Gauss ne s'applique pas simplement ici !
Autre remarque : E=0 si r<R1 et si r>R2...
Voulez vous dire qu'on ne peut pas appliquer cette méthode en supposant que le champ est egaux dans le plan de séparation entre les deux milieux .. et on peut juste dire que E=0 si r<R1 ou r>R2
La nouvelle expression fournie est correcte du point de vue de l'homogénéité. Je pense avoir compris le point de vue du correcteur de l'exercice. Quant à être d'accord avec lui...
1° Il suppose le champ radial : cela me paraît correct si l'épaisseur d = R2-R1 est petite devant R1 et R2 car on sait que le vecteur champ est normal à une surface métallique chargée au voisinage immédiat de celle-ci.
2° Pour une sphère de rayon r donné (R1<r<R2), le fait que le vecteur champ soit radial, couplé aux relations de continuité/discontinuité du vecteur champ à l'interface entre deux isolants différents ,conduit bien au fait que le vecteur champ ne subit pas de discontinuité en passant de l'isolant au vide.
3° Ce qui me gêne : dans l'application du théorème de Gauss, l'auteur suppose que E a même valeur en tout point de chaque demie sphère de rayon r. Cela me parait très osé dans la mesure où le centre O n'est pas centre de symétrie pour le condensateur. On peut s'en convaincre en montrant que l'hypothèse de l'auteur conduit à une distribution de la charge q sur la sphère de rayon R1 non uniforme. Selon l'hypothèse de l'auteur, le vecteur champ en r = R1+ a pour expression :
La densité surfacique de charge sur la demie sphère en contact avec l'isolant est donnée par le théorème de Coulomb :
La densité surfacique de charge sur l'autre demie sphère est :
On remarque : . Cela confirme bien que la répartition de charge n'est pas à symétrie sphérique ; d'où le caractère abusif souligné déjà...
Annuler
connectez vous