Je pense qu'il s'agit de calculer la

. . . .  calculer la perte d'énergie électrique entre l'état initial et l'état final du condensateur, cette perte correspondant à la dissipation d'énergie non électrique (effet Joule).
1. L'énergie du condensateur, qui vaut initialement  1/2 C², se réduit finalement à 1/8 C². La perte d'énergie est donc égale à  3/8 C².
2. Ce cas est plus délicat. Peut-être conviendrait-il de distinguer deux phases dans l'expérience , la transition correspondant au passage par zéro de la tension aux bornes du condensateur.

Pourrais tu m'expliquer en fait ce qu'il se passe dans le second cas.
Je n'arrive pas à comprendre ce que ça va changer de brancher la borne - avec l'électrode chargée positivement ???

Bonjour,
Ce qui se passe dans le second cas ?...
On a un condensateur chargé à -/2 qui se retrouve chargé à +/2. Autrement dit, on inverse la tension aux bornes du condensateur (dans un circuit de résistance nulle apparemment). Au départ, on a donc une tension en court-circuit (la tension du générateur et du condensateur s'ajoutent puisqu'elles sont en série). A priori, le courant est infini à t = 0.
Au départ, on a une énergie de C²/8 emmagasinée dans le condensateur, et, à la fin, une énergie de C²/8 emmagasinée dans le condensateur. Donc, apparemment, bilan énergétique nulle... Mais est-ce pour autant qu'il n'y a pas eu d'énergie consommée dans le circuit ?...
Ce qui complique encore les choses, c'est la résistance nulle du circuit... Comment pourrait-on avoir un effet Joule dans une résistance nulle ?...
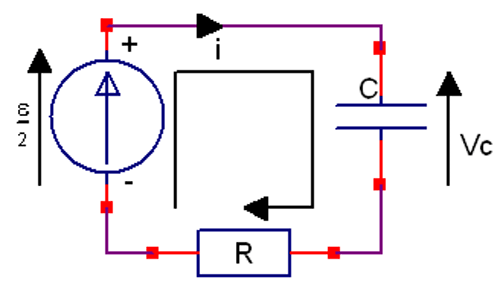
Alors, pour répondre, à cette question, je propose de modifier le circuit en ajoutant une résistance R en série. Puis on fera tendre cette résistance vers 0.
Le circuit est donc sur le schéma joint.
La loi des mailles s'écrit :

Et :

Donc :



Equation différentielle que l'on sait résoudre en terminale...
Ensuite, on peut calculer :

Et on a :

D'où :
et on fait tendre R vers 0...
Et c'est là que la surprise nous attend... Va-t-on trouver 0 ?

Si tu as quelques difficultés avec les calculs, je t'écrirai la solution en entier...

"bilan énergétique nulle" ==> bilan énergétique nul

Il y a une virgule en trop...
"pour répondre, à cette question" ==> pour répondre à cette question

J'ai fait une petite erreur... Le condensateur est chargé à et non pas à /2. Donc, au départ, on a une tension de 3/2 en court-circuit et non pas .
Mais ça ne change rien au raisonnement général. Ce ne sont que les conditions initiales...

Donc le bilan énergétique n'est pas nul...
On part d'une énergie pour arriver à  .
Mais ça aurait été plus drôle dans le cas que j'ai pris...

La réponse finale est censé être 9C²/8

Pardon

Ce ne serait pas plutôt ?

cas 2 :



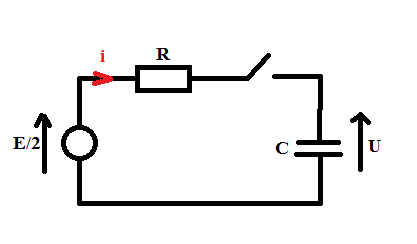
On ferme l'interrupteur en t = 0 et on a U(0) = -E

E/2 = Ri + U
i = C dU/dt

0 = R.di/dt + dU/dt
R.di/dt + i/C = 0
di/dt + i/(RC) = 0 avec i(0) = 3E/(2R)

i(t) = (3E/(2R)) * e^(-t/(RC)

Pertes joule dans R = S(de 0 à +oo) Ri² dt (avec S pour le signe intégral)

S(de 0 à +oo) Ri² dt = (3E/(2R))²*R. S(de 0 à +oo) e^(-2t/(RC) dt

= -(3E/(2R))²*R * RC/2 * [e^(-2t/(RC)](de 0 * +oo)

= -(3E/(2R))²*R * RC/2 * (-1)

= (3E/(2R))²*R * RC/2 = et ceci quel que soit la valeur de R (donc même pour R --> 0)

Sauf distraction.  

Zut pour l'orthographe.  

Oui effectivement...

J'avais perdu un 2 dans mes calculs...