Niveau licence

Composition de torseurs cinématiques

Posté par
Plukrax 08-11-11 à 21:26

Salut à tous
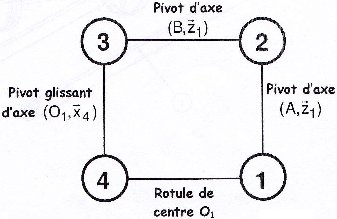
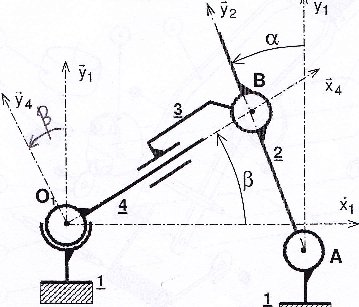
Je bloque sur un devoir de cinématique portant sur l'étude d'une pompe à pied avec manomètre de type Maxidone, dont voici le graphe de liaisons ainsi que le schéma cinématique.
On nous donne :
$\vec{O_1A}=a\vec{x_1}-b\vec{y_1}$
$\vec{AB}=c\vec{y_2}$
et $\vec{O_1B}=\lambda_{(\alpha)}\vec{x_4}$ .
Dans une première partie j'ai calculé $\lambda_{(\alpha)}$ en fonction du paramètre d'entrée du mécanisme $\alpha$ , ainsi que $\vec{V}(B,3/4)$ en fonction de $\alpha$ et de $\dot{\alpha}$ . Tout cela grâce à des relations géométriques (Chasles, etc.).
Dans la deuxième partie on nous demande d'exprimer les torseurs cinématiques {V_4/3}, {V_3/2}, {V_2/1} et {V_4/1}, chacun au point O₁ et dans la base $b_1=(\vec{x_1}, \vec{y_1}, \vec{z_1})$ , puis d'écrire une relation de composition des torseurs traduisant la fermeture cinématique du graphe de structure, au même point et dans la même base.
J'ai trouvé :
${V_{4/3}}=\left\lbrace\begin{matrix} \omega_{4/3}^x.cos\beta&V_{4/3}^x.cos\beta \\ \omega_{4/3}^x.sin\beta&V_{4/3}^x.sin\beta \\ 0&0\end{matrix}\right\rbrace_{(O_1, b_1)}$
${V_{3/2}}=\left\lbrace\begin{matrix} 0&\lambda.sin\beta.\omega_{3/2}^z \\ 0&-\lambda.cos\beta.\omega_{3/2}^z \\ \omega_{3/2}^z&0\end{matrix}\right\rbrace_{(O_1, b_1)}$
${V_{2/1}}=\left\lbrace\begin{matrix} 0&-\dot{\alpha}.b \\ 0&-\dot{\alpha}.a \\ \dot{\alpha}&0\end{matrix}\right\rbrace_{(O_1, b_1)}$
et
${V_{4/1}}=\left\lbrace\begin{matrix} \omega_{4/1}^x&0 \\ \omega_{4/1}^y&0 \\ \omega_{4/1}^z&0\end{matrix}\right\rbrace_{(O_1, b_1)}$

ensuite je compose : $\{V_{4/3}\}+\{V_{3/2}\}+\{V_{2/1}\}+\{V_{1/4}\}=\{0\}$
et je trouve les équations suivantes :
pour la rotation : $\left\lbrace\begin{array}l \omega_{4/3}^x.cos\beta-\omega_{4/1}^x=0 \\ \omega_{4/3}^x.sin\beta-\omega_{4/1}^y=0 \\ \omega_{3/2}^z+\dot{\alpha}-\omega_{4/1}^z=0 \end{array}$
et pour la vitesse : $\left\lbrace\begin{array}l V_{4/3}^x.cos\beta+\lambda.sin\beta.\omega_{3/2}^z-\dot{\alpha}.b=0 \\ V_{4/3}^x.sin\beta-\lambda.cos\beta.\omega_{3/2}^z-\dot{\alpha}.a=0 \end{array}$

Ensuite on nous demande quelles inconnues il est impossible de calculer, s'il est possible de trouver d'autres équations en permettant le calcul, puis de montrer que ces inconnues peuvent toutes s'exprimer en fonction de $\omega_{4/3}^x$ . Cette vitesse de rotation (mobilité interne de la pompe) est par la suite considérée comme nulle.
Il faut ensuite exprimer les inconnues en fonction de $\dot{\alpha}$ et des autres paramètres géométriques constants ou variables.
Finalement on doit calculer $\vec{V}(B,3/4)$ en fonction de $\dot{\alpha}$ et des autres constantes géométriques.

Je n'arrive pas à résoudre ces questions. J'ai essayé de tout exprimer en fonction de $\omega_{4/3}^x$ , je prend par exemple $cos\beta=\frac{\omega_{4/1}^x}{\omega_{4/3}^x}$ , mais si $\omega_{4/3}^x=0$ alors cela n'a plus de sens .
Bref je patauge complètement, si vous pouviez me donner quelques pistes ce serait super sympa de votre part.

Pour info, dans la première partie, j'ai trouvé : $\lambda_{(\alpha)}=\sqrt{(c.cos\alpha-b)^2+(a-c.sin\alpha)^2}$ ainsi que $\vec{V}(B,3/4)=\frac{\dot{\alpha}.c.(b.sin\alpha-a.cos\alpha)}{\lambda_{(\alpha)}}\vec{x_4}$ , mais j'ignore s'il sont à utiliser dans la seconde partie.

Merci d'avance pour votre réponse

Composition de torseurs cinématiques