Niveau autre

variation spatiale de la pression

Posté par
iSirrol 28-05-15 à 19:29

bonjour

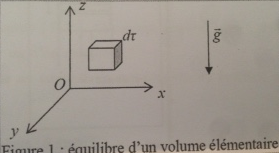
j'ai un volume elementaire $\mathrm{d}\tau=\mathrm{d} x\mathrm{d} y\mathrm{d} z$ d'eau de mer
on note $P(x,y,z)$ la pression de l'eau en un point de coordonées $(x,y,z)$

1- On me demande le bilan des actions mécanique qui s'exerce sur ce système

ma reponse : -force volumique $\mathrm{d}\vec{F_{v}}=\vec{f_v}\mathrm{d}\tau$
- force de pression $\mathrm{d}\vec{F_{p}}=-\vec{grad}p.\mathrm{d}\tau$

dites moi si c'est complet ou juste

2- On me demande de montrer que la pression est indépendante des coordonnées $x$ et $y$

j'ai l'intuition peut etre éronée quil faut chercher du coté de :

force de pression exercée sur la face horizontale situé en $z$ (bas) : $\mathrm{d}\vec{F_{pz1}}=P(x,y,z)\mathrm{d} x\mathrm{d} y.\vec{u_z}$
force de pression exercée sur la face horizontale situé en $z+\mathrm{d} z$ (haut) : $\mathrm{d}\vec{F_{pz2}}=-P(x,y,z+\mathrm{d} z)\mathrm{d} x\mathrm{d} y.\vec{u_z}$

donc $\mathrm{d}\vec{F_{pz}}=[P(x,y,z)-P(x,y,z+\mathrm{d} z)]\mathrm{d} x\mathrm{d} y.\vec{u_z}$
d'après la formule de Taylor $\mathrm{d}\vec{F_{pz}}=[\dfrac{\partial p}{\partial z}\mathrm{d} z]\mathrm{d} x\mathrm{d} y.\vec{u_z}=\dfrac{\partial p}{\partial z}\mathrm{d}\tau.\vec{u_z}$

de quoi on déduit :
$\mathrm{d}\vec{F_{px}}=\dfrac{\partial p}{\partial x}\mathrm{d}\tau.\vec{u_x} \\ \mathrm{d}\vec{F_{py}}=\dfrac{\partial p}{\partial y}\mathrm{d}\tau.\vec{u_y}$

Comment prouver à partir de ça l'indépendance que l'on cherche à démontrer ...

variation spatiale de la pression

Posté par re : variation spatiale de la pression 28-05-15 à 22:01

L'expression des forces de pressions selon les différentes directions est correcte (au signe près...)

Maintenant, expression du poids s'exerçant sur l'élément de volume ( en introduisant la masse volumique de l'eau) ?

Puis application du principe fondamentale de la statique (élément en équilibre).

Posté par re : variation spatiale de la pression 28-05-15 à 22:45

Je pense que le problème que je traite est formulé d'une façon à ne pas utiliser le principe fondamentale de la statique maintenant.

sachant que montrer que la pression est indépendante des coordonnées $x$ et $y$
vient juste après l'établissement des actions mécaniques extérieures et juste avant donner l'expression de la résultante des forces s'exerçant sur $\mathrm{d}\tau$ . En déduire la relation fondamentale de la statique des fluides $\dfrac{\mathrm{d}P}{\mathrm{d}z}=-\rho g$

Posté par re : variation spatiale de la pression 28-05-15 à 23:58

Dans ce cas, je ne vois pas : il est difficile d'établir ce résultat qui est essentiellement lié à la verticalité du champ de pesanteur sans relier la pression au poids via le PFS.

Y a-t-il des hypothèses supplémentaires sur la géométrie du problème (par exemple : étendue infinie) ?

Une telle hypothèse est parfaitement inutile pour établir le résultat mais si l'on ne te laisse pas le choix des outils...

Posté par re : variation spatiale de la pression 01-06-15 à 21:57

Bonsoir

Je pense que tu avais raisons par rapport à ce qu'il fallait faire ...

les forces qui s'appliquent sur notre volume ${\rm d} \tau$ sont :
- des forces de pression : $- \, \overrightarrow{\rm grad} \, P \cdot \rm d \tau$
- l'action de la pesanteur : $\rho\rm d\tau\vec{g}$

Principe fondamentale de la dynamique en référentiel galiléen : $- \, \overrightarrow{\rm grad} \, P \cdot {\rm d} \tau + \rho \, {\rm d} \tau \overrightarrow{g} = \vec 0 \Rightarrow \boxed{\overrightarrow{\rm grad} \, P = \rho \vec{g}}$

Notre fluide est supposé incompressible ( $\rho$ est constant) et qu'on est à la surface de la Terre ( $g$ est constant). Le référentiel proposé est cartésien, le gradient s'exprime facilement : $\vec{\rm grad} \, P = \left ( \frac{\partial P}{\partial x} \right )_{y,z} \cdot \vec{u_x} + \left ( \frac{\partial P}{\partial y} \right )_{x,z} \cdot \vec{u_y} + \left ( \frac{\partial P}{\partial z} \right )_{x,y} \cdot \vec{u_z}$$$

On a donc l'équation : $\overrightarrow{\rm grad} \, P = \rho \vect{g} \Rightarrow \left ( \frac{\partial P}{\partial x} \right )_{y,z} \cdot \overrightarrow{u_x} + \left ( \frac{\partial P}{\partial y} \right )_{x,z} \cdot \overrightarrow{u_y} + \left ( \frac{\partial P}{\partial z} \right )_{x,y} \cdot \overrightarrow{u_z} = - \, \rho \, g \cdot \overrightarrow{u_z}$

Sous forme matricielle, c'est encore plus évident de voir là où on veut en venir : $\begin{pmatrix} \\ \left ( \frac{\partial P}{\partial x} \right )_{y,z}\\ \\ \left ( \frac{\partial P}{\partial y} \right )_{x,z}\\ \\ \left ( \frac{\partial P}{\partial z} \right )_{x,y} \\ \end{pmatrix} = \rho \cdot \begin{pmatrix} \\ 0\\ \\ 0\\ \\ - g \\ \end{pmatrix}$$$

Les deux premières lignes permettent de conclure : $\left ( \frac{\partial P}{\partial x} \right )_{y,z} = \left ( \frac{\partial P}{\partial y} \right )_{x,z}=0$
La pression $P$ est donc indépendante des coordonnées $x$ et $$y$.$

____________________________________________________________________________________________________

Je dois trouver l'expression de la résultante des forces en fonction de $g,~\rho(z),~P(z),~P(z+\mathrm{d}z),~\mathrm{d}x,~\mathrm{d}y,~\mathrm{d}z$ et $\vec{u_z}$ , en déduire $\dfrac{\mathrm{d}P}{\mathrm{d}z}=-\rho g$