Inscription / Connexion Nouveau Sujet
Machine d'Atwood
Bonjour,
Deux points matériels M1 et M2 de masse m1 et m2 sont reliés par un fil de masse négligeable autour d'une poulie de rayon R
1. Représenter les forces appliquées au système de deux points matériels
2. Appliquer le théorème du moment cinétique et en déduire l'accélération m1
3. En déduire l'expression de la tension T du fil
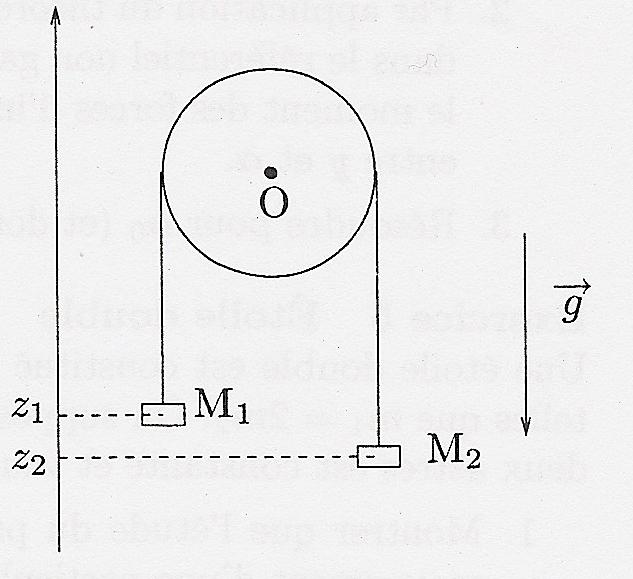
1. Les forces appliquées au système des deux points matériels sont le poids P et la tension du fil T
2. Donc
D'après le premier théroème de Koenig, on a
Et ensuite, je bloque ^^
Une petite piste s'il vous plait

Merci

Skops

On a négligé, je suppose le moment d'inertie de la poulie (cela aurait du être précisé dans l'énoncé).
Force motrice (sens descente de m1) = g(m1 - m2)
Cette force met les 2 masses en mouvement.
g(m1 - m2) = (m1+m2).a
a = g(m1 - m2)/(m1 + m2)
Donc force agissant sur m1: F = m1.a = m1.g(m1 - m2)/(m1 + m2)
Or on a aussi : F = m1.g - T
--> m1.g(m1 - m2)/(m1 + m2) = m1.g - T
T = m1.g(1 - (m1 - m2)/(m1 + m2))
T = m1.g(m1 + m2 - m1 + m2)/(m1 + m2)
T = 2.m1.m2.g/(m1 + m2)
-----
Sauf distraction. 
Salut JP 
Plusieurs questions ^^
- Tu saurais le faire avec le théorème du moment cinétique ?
- Comment as tu trouvé la force motrice ? c'est à savoir ?
- g(m1-m2)=(m1+m2)a est ce que ca vient du PFD ? (parce que je ne vois ni le poids, ni la tension du fil)
Skops 
Approche un peu différente (plus intuitive qu'en employant des thèorèmes sans bien en sentir la portée-.
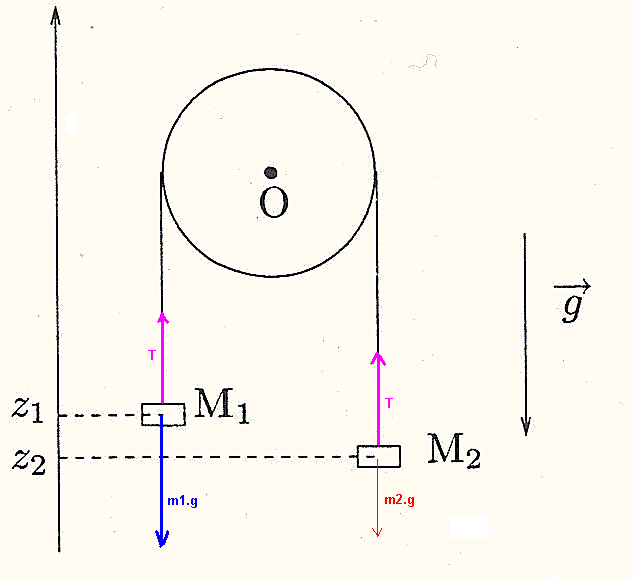
Résultante des forces sur M1, (vers le bas)
F1 = m1.g - T
et donc avec a1 l'accélération de M1 vers le bas: F1 = m1.a1
--> m1.a1 = m1.g - T
a1 = g - (T/m1)
-----
Résultante des forces sur M2, (vers le bas)
F2 = m2.g - T
et donc avec a2 l'accélération de M2 vers le bas: F2 = m2.a2
--> m2.a2 = m2.g - T
a2 = g - (T/m2)
-----
Mais, on a évidemment a1 = -a2 puisque les masses sont reliées par un fil via la poulie.
-->
g - (T/m2) = -g + (T/m1)
(T/m1) + (T/m2) = 2g
T(m1 + m2)/(m1.m2) = 2g
T = 2g.m1.m2/(m1+m2)
-----
Et on retrouve alors:
a1 = (-a2) = g - (T/m1) = g - 2g.m2/(m1+m2)
a1 = g(m1+m2-2m2)/(m1+m2)
a1 = g(m1-m2)/(m1+m2)
C'est l'accélération vers le bas de M1 (et évidemment celle de M2 vers le haut).
-----
En fait, j'ai utilisé le théorème des moments cinétiques sans l'écrire formellement.
Si on veut vraiment pouvoir le citer, il faut d'abord avoir la définition qu'on en a donné car il y différente manière de l'exprimer (équivalentes).



