Inscription / Connexion Nouveau Sujet
Vitesse et direction vent - Relativité restreinte
Bonjour, cela fait depuis plusieurs jours que je bloque sur un exercice :
Un bateau navigue dans un courant de 5km/h et de 15° (angle de 15° par rapport au nord). La vitesse du bateau par rapport à l'eau est de 10km/h et de 310°. A bord, on mesure un vent apparent de 40km/h et de 350°.
Quel est la vitesse et la direction du vent par rapport au sol ?
Ce que je sais : vent apparent : combinaison du vent réel et du vent vitesse.
Je pose :
Vc = 5km/h, Vb = 10km/h, VA = 40km/h
 c = 15°,
c = 15°,  b = 310°,
b = 310°,  A = 350°.
A = 350°.
Je cherche  V qui est la direction du vent et VV la vitesse du vent.
V qui est la direction du vent et VV la vitesse du vent.
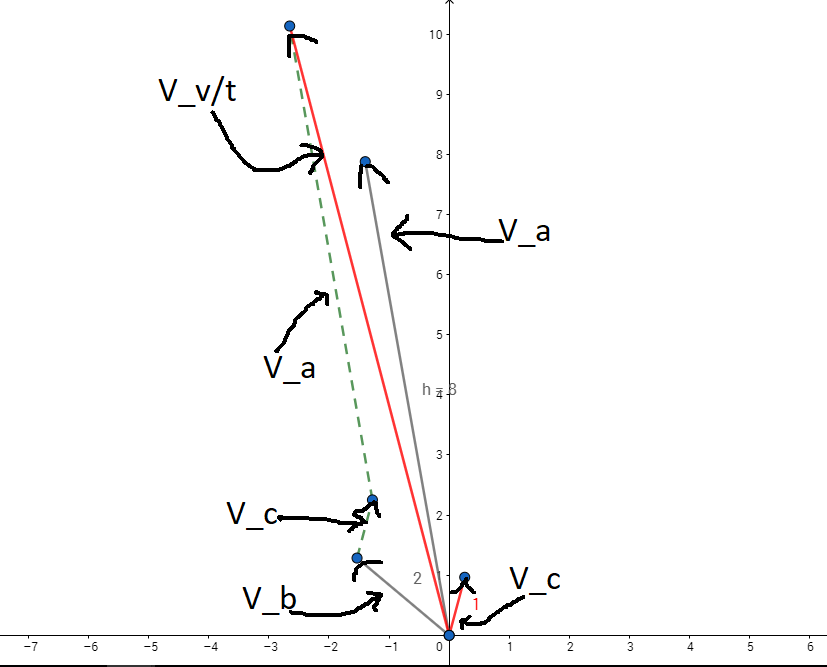
J'ai essayé de faire un schéma mais il y a 2 phrase que je comprend mal dans l'énoncé :
"La vitesse du bateau par rapport à l'eau" -> Pour tracer le vecteur vitesse du bateau, on doit faire un angle de 310° mais en partant du Nord de la rose des vents ou en partant du vecteur vitesse courant ?
"A bord, on mesure un vent apparent de 40km/h et de 350°." Doit on ici partir du nord de la rose des vents ou partir du vecteur vitesse du bateau pour avoir un angle de 310° ?
Bonsoir
À des vitesses aussi faibles, la théorie de la relativité n'a pas d'intérêt. Il s'agit d'un simple problème de composition des vitesses. Tu peux caractériser chaque direction par son angle avec un axe orienté vers le nord. Écrire les relations vectorielles et projeter...
Relations de composition des vitesses :
La vitesse du vent par rapport à un repère terrestre (vitesse absolue) est la somme vectorielle de la vitesse du vent par rapport au bateau (vitesse du vent relatif) et de la vitesse du bateau par rapport au repère terrestre.
La vitesse du bateau dans le repère terrestre (vitesse absolue) est la somme vectorielle de la vitesse du bateau par rapport à l'eau (vitesse relative) et de la vitesse de l'eau par rapport au repère terrestre (vitesse du courant).
Tu devrais pouvoir te débrouiller seul avec cela ! Ce genre d'exercice figure aux épreuves de permis bateau et ce permis n'est pas passé que par des scientifiques !
Tu risques de te compliquer la vie ! Utilise la méthode de projection que tu utilises habituellement dans un problème de statique ou de dynamique. En combinant les deux relations précédentes, la vitesse que tu cherches est :
Projette cette relation sur un axe (Ox) orienté vers l'est et un axe (Oy) orienté vers le nord. Les normes et les orientations des trois vecteurs à droite du signe « = » sont connus. Tu vas obtenir un système à deux inconnues : la norme du vecteur et l'angle
 entre l'axe (Oy) et ce vecteur...
entre l'axe (Oy) et ce vecteur...
Si tous les angles sont mesurés à partir de l'axe (Oy), le sens positif étant, comme en marine, le sens des aiguilles d'une montre. Cela donne tout simplement, avec mes notations que je trouve plus explicites :
deuxième formule analogue en remplaçant les sinus par des cosinus. En laissant les vitesses en km/h et les angles en degrés, on obtient :
Évidemment, certains angles peuvent être remplacés par leur complémentaire ou leur supplémentaire mais cela complique inutilement à mon avis.
Je te laisse terminer. Avec la convention d'orientation d'angle choisi, tu devrais obtenir une valeur de  voisine de -15°C soit environ 345°...
voisine de -15°C soit environ 345°...
Je te laisse vérifier tes calculs...