Inscription / Connexion Nouveau Sujet
Vitesse de réaction
Bonjour à tous,
Me revoici avec des exercices de chimie concernant les vitesses de réactions (cinétique).
Voici l'énoncé:
"On met de l'éthylamine (C2H5NH2) dans un récipient vide à la température de 500°C. Décomposition suivant la réaction:
C2H5NH2(g) --> (réaction partielle) C2H4 (g) + NH3(g).
A t=0, la pression est de 5mmHg
Le volume reste constant, on mesure la pression totale au cours du temps. Les résultats:
t = 0 min --> P = 55 mmHg
t = 1 min --> P = 60 mmHg
t = 4 min --> P = 72 mmHg
t = 10 min --> P = 89 mmHg
On nous demande de vérifier que la réaction est de premier ordre en calculant la constante de vitesse".
Pour la résolution je ne parviens pas à comprendre quel raisonnement utilisé.
Si nous utilisons la loi des gaz parfaits, nous pouvons déterminer n(C2H5NH2)
PV = nRT
V est constant et T est constante
P = nR
n = P/R
Ainsi à
t= 0 --> P = 7332,7 Pa --> n = 882,39 moles
t= 1 --> P = 7999,32 Pa --> n = 962,61 moles
t= 4 --> P = 9599,184 Pa --> n = 1155,14 moles
t= 10 --> P = 11 865 Pa --> n = 1427,8 moles
Je pense que mon raisonnement n'est pas bon, les quantités de matière semblent beaucoup trop importantes, je suis bloquée pour la suite.
Pour la cinétique de premier ordre du type A --> P ou A + B --> P
v = k x [A]
[A] = [A]initiale x e ^(-k x t)
et t1/2 = ln2/k
Quelqu'un aurait la gentillesse de m'aider?
merci par avance
Cordialement
Bonjour
Si on note x l'avancement à la date t, la quantité totale de gaz est alors (no+x) (remplis un tableau d'avancement pour t'en convaincre).
Puisque la vitesse de réaction est définie par :
tu devrais te débrouiller maintenant !
Tu obtiens des quantités de gaz (en moles) beaucoup trop grandes... Tu as sans doute oublié d'exprimer le volume en m3...
J'ai oublié un "Po" dans l'expression de la pression à la date t. Simple étourderie de copie sous Tex car les formules qui suivent sont correctes. Je rectifie quand même :
Merci Vanoise,
Je ne comprends pas pourquoi la quantité de gaz totale vaut (n0 + x).
Si je fais un tableau d'avancement à t
C2H5NH2 --> C2H4 + NH3
n0 --> 0 + 0
n0 -x --> x + x
Par ailleurs je ne comprends pas non plus:
P(t) = (n0 + x) RT/V = (P0 + x) RT/V
Enfin si je comprends qu'il faut appliquer la loi des gaz parfaits mais ne comprends pas pourquoi n0 + x = P0 + x

merci par avance
Je viens de comprendre.
Prenons un volume constant = 1L soit 0,001 m3
P0 = n0 . RT/V
A t, la quantité de gaz totale est égale à (n0-x)+x+x soit (n0+x)
de ce fait
P(t) = (n0+x).RT/V
P(t) = (n0.RT/V) + (x.RT/V)
P(t) = P0 + (x.RT/V)
A partir de là nous pouvons déterminer x pour chaque t.
x = [V(P(t)-P0)] / RT
t = 0 --> P = 7332,7 Pa --> x = 0 mole
t = 1 --> P = 7999 Pa --> x = 0,0001 mole
t = 4 --> P = 9599 Pa --> x = 0,00035 mole
t = 10 --> P = 11865 Pa --> x = 0,0007 mole
Par contre je suis bloquée pour la suite.
J'ai trouvé l'avancement x = [NH3] = [C2H4]
v = d[NH3]/dt
v = 0,00007 mol/min
Je ne vois pas comment déterminer ensuite k puis l'ordre de la réaction 
Sachant que je n'ai pas la concentration initiale de C2H5NH2.
L'extrait de tableur ci-dessous devrait t'aider. J'ai tout simplement utilisée le résultat précédemment obtenu :
en faisant attention au fait que on obtient la concentration ainsi en mol/m3 ; il faut convertir en mol/L.
En notant co la concentration initiale en éthylamine, une cinétique du premier ordre conduit à :
d'où l'usage dans le tableur d'un logarithme népérien...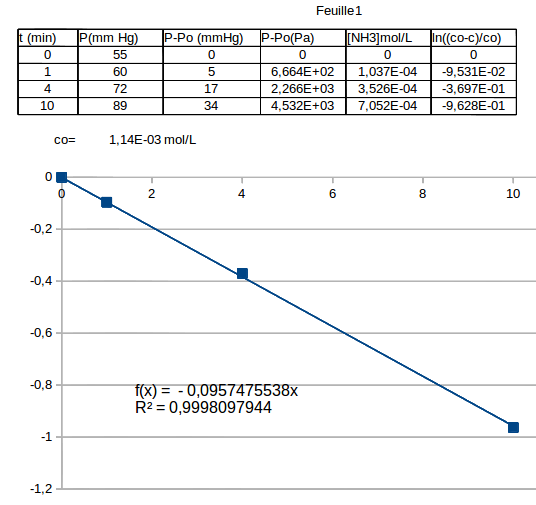
***Image recadrée***
Merci Vanoise,
Comment arrivez vous à déterminer Co (concentration initiale en éthylamine)?
Par ailleurs comment calculez vous ln[(Co -C)/Co] = -kt puisque nous ne connaissons ni Co ni k?
En fait je pense ne pas comprendre le but de l'exercice ni ce qu'on me demande réellement :/
La concentration initiale en éthylamine co s'obtient facilement à partir de la pression initiale :
On place ensuite dans un repère les points expérimentaux d'abscisses t et d'ordonnées ln[(Co -C)/Co].
Un programme de régression linéaire permet de montrer que ces points sont, en excellente approximations, alignés avec l'origine comme le prévoit l'étude théorique précédente ; cela fournit deux renseignements :
1° : La cinétique est bien d'ordre 2 ;
2° : la valeur absolue du coefficient directeur est la valeur de k : 9,57.10-2min-1
Merci Vanoise,
En fait on ne peut deduire l'ordre de la cinétique qu'en utilisant un graphique?
Vous précisez que l'ordre est de 2.
Cependant si nous utilisons le logarithme neperien, l'ordre de la réaction n'est elle pas de l'ordre 1?
Je récapitule la démarche.
1° l'énoncé émet l'hypothèse d'un ordre partiel égal à un pour chaque réactif (ordre global égal à 2)
2° la théorie permet d'affirmer que, si l'hypothèse est correcte, alors :
ln[(Co -C)/Co] = -kt
3° pour savoir si l'hypothèse est correcte, on réalise l'expérience décrite dans l'énoncé puis on trace le graphe. Puisque les points sont alignés avec l'origine, cela prouve :
* l'hypothèse d'un ordre global égal à 2 est bien vérifiée ;
* le coefficient directeur de la droite moyenne permet d'obtenir k.
La méthode est très rapide avec un tableur ou une calculatrice graphique de bon niveau, sinon...
Merci Vanoise pour la synthèse
Cependant peut-on nous demander ce genre d'exercice à un examen sachant que nous n'aurons ni tableur (excel) ni calculatrice graphique?
Ce qui me parait un peu compliqué si nous n'avons pas ce genre d'instrument.
Si tel est le cas, nous devons donc faire un graphique à la main, choisir 2 points et calculer la pente pour en déduire le k. Est ce correct?


