Inscription / Connexion Nouveau Sujet
vitesse d'une bille dans un tube en rotation
Bonjour, je suis nouveau sur le site.
Je me pose une question, et j'espère qu'il est possible d'y répondre.
Je voudrais déterminer la vitesse d'une bille qui fait des allers-retours dans un tube en rotation.
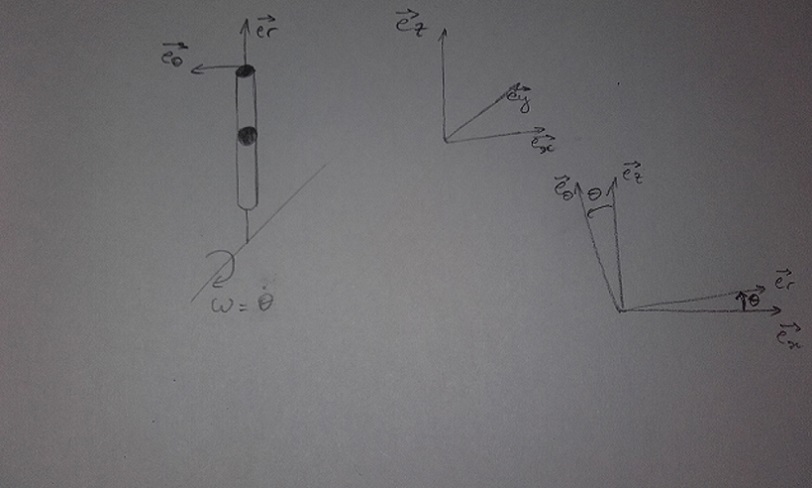
L'axe de rotation est horizontal. J'accroche un repère de coordonnées polaires à mon tube (er,ez) qui fait un angle théta avec le repère cartésien associé à mon laboratoire, référentiel galiléen de l'étude.
J'ai fait un inventaire des forces s'exerçant sur ma bille, pouvez-vous me confirmer s'il est bon et complet :
le poids P=mg. je le projette sur er et je trouve :
P=-m*g*sin(théta)
la force centrifuge, portée par er : F=(m*v^2)/r
Je décide de négliger les forces de frottements.
avec : v=omega*r
omega : vitesse de rotation de mon tube omega = théta point.
r : distance par rapport à l'axe de rotation de la bille
m : masse de la bille
je projette le PFD sur er et j'obtiens : m*a=(m*v^2)/r-m*g*sin(théta)
je ne sais pas si mon raisonnement est correct, pouvez-vous m'aiguillez?
Je vous remercie d'avance pour vos réponses à venir.
Hello
Ne dois tu pas considérer la réaction de la paroi du tube sur la bille, lorsque elles sont en contact l'une avec l'autre?
Salut,
Non, il n'y a pas de réaction du support sur er.
Mis à part ça, penses-tu que l'équation que je trouve est correcte? Je trouve une équation différentielle que je ne peux pas intégrer, c'est la misère =(.
Mets donc, sur le site, un énoncé complet ... et le dessin qui l'accompagne.
Avec ce que tu as écris, il y a de multiples manières d'interpréter l'exercice.

Bonjour,
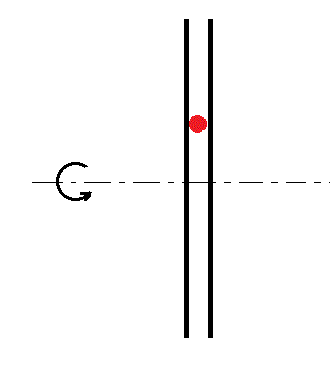
Un tube tourne autour d'un axe horizontal à une vitesse angulaire constante omega.
Ce tube est fermé en ses deux extrémités et contient une bille qui peut faire des allers-retours dans le tube.
Déterminer les forces qui s'exercent sur la bille.
Déterminer l'équation du mouvement de la bille.
Merci beaucoup =)
Je n'arrive pas à charger l'image, mais oui, c'est ça. Par contre, le tube est fermé aux extrémités.
Dans un référentiel lié à la bille :
- Poids de la bille.
- Force centrifuge.
Et ... si la bille a le même diamètre que le tube : les pressions des 2 cotés de la bille dans le tube varient avec la position de la bille ... sauf si le tube est vide d'air.
Faut-il tenir compte de cela ?

Le diamètre de la bille est plus petit que celui du tube, donc je pense qu'on peut négliger les efforts de pression. Qu'en penses-tu?
Hello
Je persiste à croire que la réaction du tube sur la bille ne peut être ignorée: lorsqu'elle est nulle (diamètre de la bille inférieur à celui du tube) la composante de la vitesse ne l'est pas. Outre les frottements négligeables et les extrémités fermées, on fait d'autres hypothèses sur la configuration de ce système?
On ne peut pas négliger la réaction du tube sur le bille ...
Evidemment puisque c'est grâce à elle que la bille est entraînée dans sa rotation avec le tube.
Cela dit, cette réaction du support (hors frottement) est toujours perpendiculaire à l'axe du tube ... et donc n'entre pas en considération directement dans le mouvement de la bille le long de l'axe du tube.
Dans un référentiel lié à la bille :
Fc = m.w².x
Composante du poids suivant Ox : F1 = -m.g.sin(theta) (avec theta = -wt + Phi, Phi étant l'angle en t = 0)
La résultance des forces sur la bille (suivant Ox) est F = m.w².x + mg.sin(theta)
On a donc (si la bille n'est pas à butée) : m.w².x + mg.sin(theta) = m.d²x/dt²
d²x/dt² - mw²x = -mg.sin(theta)
d²x/dt² - w²x = -g.sin(-wt + Phi)
Pour simplifier, on choisira Phi = 0 et alors : d²x/dt² - w².x = g.sin(wt)
MAIS ...
On remarquera que sur un tour complet, la moyenne de w².x + g.sin(wt) est forcément positive (puisque le terme sinusoïdal a une valeur moyenne nulle et que x ne peut être que > 0)
Donc, l'accélération moyenne est positive avec pour conséquence que la bille doit aller toquer à butée et puis y rester sur au moins une portion de tour.
Donc l'équation trouvée est valable tant que (abscisse du début du tube) < x < (abscisse de l'extrémité du tube).
Sur la portion de tour pour laquelle on aurait eu x plus grand que l'abscisse de l'extrémité du tube (si pas de butée au tube) , on doit remplacer l'équation trouvée par x = abscisse de l'extrémité du tube et dx/dt = 0
On aura alors la bille faisant des aller-retour dans le tube mais avec la bille arrêtée par moment (sur une portion de tour)
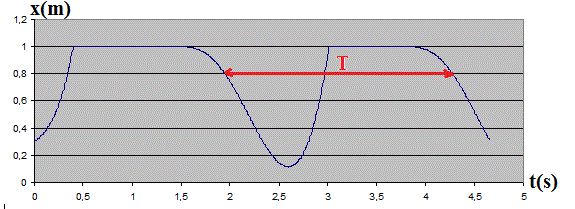
Si on tient compte de tout cela, on arrive par exemple à ceci :
Avec par exemple les valeurs numériques suivantes :
extrémité du tube à l'abscisse 1 m.
xp = 0,3 m, v(0) = 0,5 m/s , w = 2,7 rad/s et g = 9,81 m/s²
On obtient ceci :
Sauf distraction, ou erreur(s) (rien vérifié.)

euh
Vous négligez il me semble la portion du mouvement ou la bille est en chute libre (prenez le cas qui n'a pas encore été exclu par les hypothèses ou diamètre(bille) << diamètre (tube)
Cela invalide dans l'absolu il me semble
Fc = m.w².x
dans le référentiel bille
On peut tout envisager ...
Je ne pense pas cependant que ce soit attendu dans l'exercice.
Même si ce n'est pas explicitement dit, la bille a un diamètre un peu plus petit que celui du tube. On n'est pas dans le cas d'un tuyau type oléoduc avec une bille minuscule.
En tout cas, avec le dessin fourni, on n'a pas une bille à diamètre < < < diamètre du tube.
Mais c'est à totorin de le préciser.

Bonsoir
Une très modeste contribution : si on suppose le diamètre de la bille nettement inférieur au diamètre intérieur du tube, on tombe sur les difficultés soulevées par Dirac.
Si on suppose la bille de diamètre peu inférieur au diamètre intérieur du tube, la vitesse de la bille par rapport à la paroi produit un phénomène de couche limite qui fait que la bille se comporte quasiment comme un piston étanche : on tombe alors sur les difficultés signalées par JP dans son message du 18-11-16 à 15:16.
Si on ne fait pas l'hypothèse d'un tube vide d'air et d'un rayon de la bille de très peu inférieur à celui du tube, le problème est quasi insoluble...
Bonjour,
Oui le diamètre de la bille est juste légèrement inférieur au diamètre du tube. On fait aussi l'hypothèse que le tube est vide d'air. Le raisonnement de J-P me convient parfaitement.
Maintenant j'ai un petit soucis pour résoudre l'équa diff. Elle ressemble à une équation de type oscillateur harmonique (ce qui était prévisible puisqu'on s'attend à ce que la bille fasse des allers-retours dans le tube) mais avec un signe - et un second membre en sinus. Je crois que la solution s'écrit avec des cosinus et sinus hyperbolique pour le signe négatif, mais je ne sais pas comment déterminer la solution particulière, qui n'est pas constante. Pouvez-vous m'éclairer sur la question?
Merci beaucoup
d²x/dt² - w²x = g.sin(wt)
Solutions de d²x/dt² - w²x = 0
P² - x² = 0
p = +/- w
x = A.e^(wt) + B.e^(-wt)
Solution particuliére de d²x/dt² - w²x = -g.sin(wt)
x = a.sin(wt)
x'' = -aw².sin(wt)
-aw².sin(wt) - w².a.sin(wt) = g.sin(wt)
-2aw² = g
a = -g/(2w²)
x = -g/(2w²).sin(wt)
Solutions générales de d²x/dt² - w²x = -g.sin(wt) :
x = -g/(2w²).sin(wt) + A.e^(wt) + B.e^(-wt)
A et B sont des constantes dépendant des conditions initiales.
Sauf distraction. 
D'accord.
Donc en prenant comme condition initiale x=0 et x'=0, j'obtiens :
avec x=0 : A=-B
avec x'=0 : A=-g/(4w²)
Merci beaucoup pour votre aide.
Oui, mais attention que l'équation ainsi trouvée n'est valable qu'en transitoire
Par exemple avec les valeurs numériques prises avant , mais en prenant v(0) = 0 et x(0), on obtient ceci :
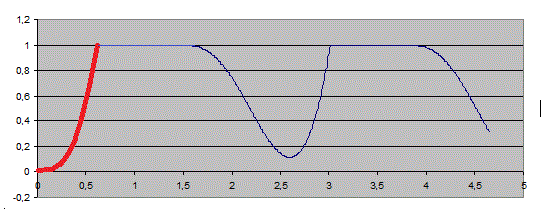
L'équation que tu auras trouvée (avec Vo = 0 et xo = 0) ne pourra représenter que la partie rouge du graphique ...

Je veux le mouvement quelque soit t et la bille est censée retombée une fois qu'elle a atteint le bout du tube, comment je fais?
En ayant corrigé l'une ou l'autre erreur de signe ...
On prenant L = 1 comme abscisse du bout du tube éloigné de l'axe de rotation.
Si on veut avoir toute la courbe d'un coup :
Résoudre : d²x/dt² - w²x = - g.sin(wt + Phi) avec Phi = arcsin(w²/g) et conditions initiales : x(0) = L (=1) et v(0) = 0
On obtient : x(t) = g/(2w²).sin(wt+phi) + A.e^(wt) + B.e^(-wt)
...
x(t) = g/(2w²).sin(wt+phi) + (1/2 - g/(4w²).(sin(Phi) + cos(Phi)).e^(wt) + (1/2 - g/(4w²).(sin(Phi) - cos(Phi)).e^(-wt)
avec Phi = arcsin(w²/g)
On aura alors (par cette équation) la courbe depuis t = 0 jusqu'au t=t1 correspondant à x(t1) = 1 ... et pour autant que x reste > 0
Pour le reste de la période, soit entre t1 et t2 = 2Pi/w, on aura x(t) = 1 et v(t) = 0 (à butée).
Avec les valeurs numériques prises au début (pour L = 1 ; w = 2,7 rad/s et g = 9,81 m/s²), on obtient alors ceci :
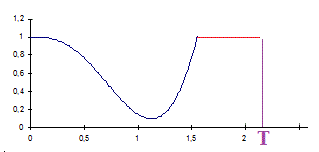
La partie en bleu correspond à :
x(t) = g/(2w²).sin(wt+phi) + (1/2 - g/(4w²).(sin(Phi) + cos(Phi)).e^(wt) + (1/2 - g/(4w²).(sin(Phi) - cos(Phi)).e^(-wt)
avec Phi = arcsin(w²/g)
La partie en rouge à été expliquée (bille à butée)
Et pour t > T, la figure se répète ...
-----
Mais, avec d'autres valeurs numériques, le comportement peut évidemment différer.
Par exemple, si w est suffisant grand (tel que w.L >= mg), alors la bille restera en permanence à butée sur l'extrémité du tube éloignée de l'axe de rotation.
Et si w est très petit, la bille fera des aller retour sur toute la hauteur du tube ... en restant un "certain temps par tour" à butée aux extrémités du tube.
Remarque, avant de "vouloir une équation qui ...", il est impératif de comprendre qualitativement physiquement ce qui se passe dans toutes les situations... sinon, je te prédis les pires ennuis par la suite.
Sauf distraction. 
Je n'ai cependant pas compris d'où vient phi = arcsin(w²/g)
Cela correspond au point où la force centrifuge avec la bille à butée est juste égale et opposée à la composante du poids suivant Ox.
Fc = m.w².L
Composante du poids suivant Ox : m.g.sin(theta)
m.w².L = m.g.sin(theta)
w².L = g.sin(theta)
sin(theta) = w²L/g
theta = arsin(w²L/g)
avec theta = wt + Phi
en t = 0 : theta = Phi = arsin(w²L/g) et comme j'ai choisi L comme unité de longueur pour faciliter les calcul ... --> Phi = arsin(w²/g)
Sauf distraction.

Bonjour,
J'ai refait les calculs et je trouve pareil. Par contre, quand je trace la x en fonction de t sur Matlab je ne trouve pas la même chose que vous. Pourquoi?
x(t) = g/(2w²).sin(wt+phi) + (1/2 - g/(4w²).(sin(Phi) + cos(Phi))).e^(wt) + (1/2 - g/(4w²).(sin(Phi) - cos(Phi))).e^(-wt)
avec Phi = arcsin(w²/g)
avec dans mon exemple : w = 2,7 rad/s , g = 9,81 N/m
Phi = arsin(2,7²/9,81) = 0,8377 rad
x(t) = g/(2w²).sin(wt+phi) + (1/2 - g/(4w²).(sin(Phi) + cos(Phi))).e^(wt) + (1/2 - g/(4w²).(sin(Phi) - cos(Phi))).e^(-wt)
x(t) = 9,81/(2*2,7²).sin(2,7.t+0,8377) + (1/2 - 9,81/(4*2,7²).(sin(0,8377) + cos(0,8377))).e^(2,7.t) + (1/2 - 9,81/(4.2,7²).(sin(0,8377) - cos(0,8377))).e^(-2,7.t)
x(t) = 0,6728.sin(2,7.t+0,8377) + 0,02488.e^(2,7.t) + 0,4751.e^(-2,7.t)
Et ceci tracé pour x dans [0 ; 1,55] donne :
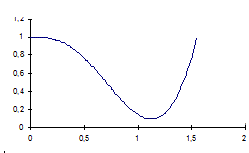

J'ai le même tracé avec vos valeurs mais la fonction n'est pas périodique, voilà ce que j'observer pour l'intervalle [0,3] :
aie aie aie.
Evidemment que x(t) = 0,6728.sin(2,7.t+0,8377) + 0,02488.e^(2,7.t) + 0,4751.e^(-2,7.t) n'est pas périodique.
J'ai expliqué que cette relation n'était valable que pour l'intervalle de temps [0 ; 1,55] s avec les valeurs numériques choisies. (1,55 s étant la valeur de t pour laquelle la bille arrivait à butée).
Qu'il fallait ensuite considérer que x(t) = 1 sur l'intervalle de temps ]1,55 ; T] avec T = 2Pi/w = 2Pi/2,7 = 2,33 s (voir mon dessin du 22-11-16 à 14:12)
Ce dessin représente donc la position de la bille dans le tube pour un tour complet du tube.
La figure du message du 22-11-16 à 14:12 doit donc être reproduite décalée de T , puis de 2T puis de 3T ... si on veut voir plus loin dans le temps.
Ce n'est évidemment pas l'équation x(t) = 0,6728.sin(2,7.t+0,8377) + 0,02488.e^(2,7.t) + 0,4751.e^(-2,7.t) qu'on doit utiliser pour t > T, il suffit de décaler le dessin comme expliqué.
Si on veut vraiment une relation valable pour t > T, alors on peut écrire :
x(t) = 0,6728.sin(2,7.(t - k.2Pi/2,7) + 0,8377) + 0,02488.e^(2,7.(t - k.2Pi/2,7)) + 0,4751.e^(-2,7.(t - k.2Pi/2,7)) pour t compris dans [k.2Pi/2,7 ; k.2Pi/2,7 + 1,55]
et x(t) = 1 pour t dans [1,55 + k.2Pi/2,7 ; (k+1).2Pi/2,7]
avec k dans N
Pour chaque valeur de k dans N ... on a la représentation de la (k+1)ème période de x(t)
-----
Attention, il est impératif de comprendre, toutes les questions que tu poses (mêmes les dernières) montrent que tu ne comprends la réalité physique qui se cache derrière les équations.
Sauf distraction. 
J'en ai une autre.
J'ai testé le modèle avec différentes valeurs de L et de omega. évidemment, quand omega est trop grand, le modèle prévoit que la bille reste en L et ne redescend pas. Par contre des fois je trouve des abscisses négative. Puis-je prendre la valeur absolue dans ce cas-là, ce qui supposerait qu'il n'y a pas d'énergie perdue due à la collision en x = 0?
"Par contre des fois je trouve des abscisses négative. Puis-je prendre la valeur absolue dans ce cas-là, ce qui supposerait qu'il n'y a pas d'énergie perdue due à la collision en x = 0?"
Bien sûr que non.
Si l'abscisse de l'extrémité du tube près de l'axe de rotation est a (avec a > 0 avec ton dessin), alors il est impossible d'avoir pour la bille des abscisses < a.
Tout comme, j'ai bloqué à x = 1 (et v = 0) si la bille allait à butée extérieure... il faut bloquer à x = a et v = 0 si la bille va à butée"intérieure" dans le tube.
Cela va sans dire ... mais cela va encore mieux en le disant.
Je ne peux que répéter une remarque déjà faite (plus qu'importante).
Attention, il est impératif de comprendre, toutes les questions que tu poses (mêmes les dernières) montrent que tu ne comprends la réalité physique qui se cache derrière les équations.
Sauf distraction. 
Bonjour,
Je ne comprends pas comment dans votre exemple avec les valeurs que vous avez prises, la bille n'atteint pas d'abscisses négatives comme vous n'avez pas pris en compte l'abscisse mini dans les conditions initiales.
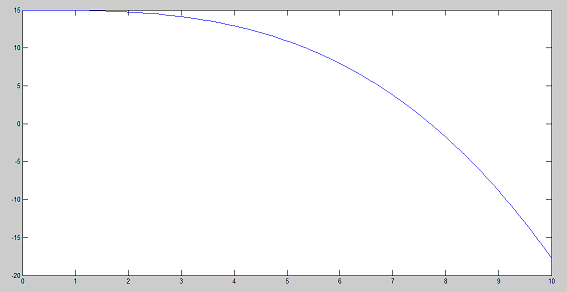
J'ai utilisé la même fonction avec omega = 0.02 rad/s L = 15 m et j'ai obtenu des abscisses négatives au bout d'un moment regardez.
Comment écrire la condition qui correspond à l'abscisse mini dans ce cas-là?
Merci pour toute l'aide que vous m'apportez
Bonjour
Une modeste contribution car je laisse JP gérer ce post.
Pour la mise en équation et l'inventaire des forces appliquées à la bille, le référentiel choisi est le tube. Ce référentiel n'étant pas galiléen, il faut faire intervenir les forces d'inertie.
La force d'inertie d'entraînement est correctement prise en compte mais il n'est pas question (sauf mauvaise lecture de ma part) de la force d'inertie de Coriolis. Pourtant celle-ci existe ici. Avec les notations du schéma fourni par totorin le 18-11-16 à 10:51 elle à pour expression :
Heureusement pour la validité de la suite de l'étude, cette force est compensée par la réaction du tube et n'intervient donc pas dans l'équation différentielle du mouvement. totorin aura sans doute dans l'année à traiter d'autres problèmes où cette force influencera le mouvement... Il vaut donc mieux ne pas l'oublier dans l'inventaire des forces !
Je ne peux que répéter ce que j'ai déjà dit.
On commence par comprendre physiquement le problème ...
Cela permet alors de manipuler les équations trouvées en prenant les précautions qui s'imposent.
Et tu ne comprends pas physiquement ce qui se passe ... donc tu n'arrives pas à résoudre correctement les différents cas.
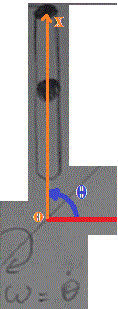
Sur le dessin du haut du message du 20-11-16 à 10:59, il est évident que l'abscisse de la bille ne peut pas être négative (sinon elle serait à l'extétieur du tube)
Si l'abscisse de l'extrémité du tube la plus proche de l'axe de rotation est "a" et que l'abscisse de l'extrémité du tube la plus éloignée de l'axe de rotation est "b", alors :
on a obligatoirement 0 <= a < b et la bille ne peut se balader que dans des abscisses comprises dans [a ; b] ... (Avec a et b POSITIFS)
Donc, l'équation donnant la position (par son abscisse) de la bille en fonction du temps ne peut être utilisée que si les abscisses sont comprises dans [a ; b]
Tant que tu n'auras pas compris (physiquement) pourquoi c'est ainsi, tu continueras à poser des questions sur de faux problèmes.

Juste pour info :
Voila par exemple ce que cela donne avec : a = 0 ; b = 1 et w = 1 rad/s
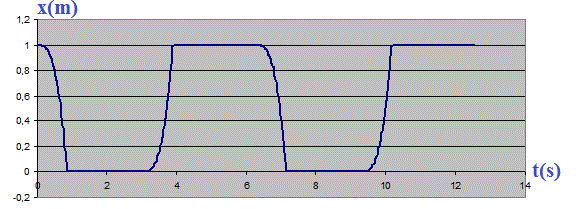
La bille fait, dans ce cas, des aller-retours sur l'entièreté du tube et reste à butée à l'une ou l'autre extrémité du tube pendant une partie du cycle.
... la bille reste évidemment dans le tube en permanence, elle n'en sort jamais.

Physiquement j'ai bien évidemment compris ce qu'il se passait, c'est une expérience très simple à réaliser.
Mon ennui est que je ne comprends pas où apparaît le a dont vous parlez dans l'équation. Dans le cas que je vous ai soumis, même si je force pour ne tracer que les points d'abscisses négatives, la courbe ne remonte jamais pour atteindre de nouveau le bout du tube.
Merci beaucoup pour votre aide 
ps : merci à Vanoise pour ses "modestes contributions" qui sont d'une grande importance

Mon ennui est que je ne comprends pas où apparaît le a dont vous parlez dans l'équation.
Il faut clamper soit même, soit par logiciel (comme dans excel), soit comme expliqué dans mon message du 23-11-16 à 11:30 pour le cas particulier traité à ce moment.
Voila par exemple un fichier excel sur ce problème :
Cellule A1 : =PI()/500/D1*2 (c'est l'incrément delta t, calculé pour que 1000 incréments correspondent à 2 tours complets du tube.
Cellule B1 : on entre la valeur de b (en m)
Cellule I2 : on entre la valeur de a (en m)
cellule c1, on entre la vitesse initiale de la bille (en m/s)
cellule D1 : on entre la pulsation (en rad/s) pour la rotation du tube
cellule E1 : on entre l'intensité de la pesanteur (en N/kg)
Cellule F2 : =ASIN(D1^2*1/E2) (calcul de Phi pour être en t = 0 juste où la force centrifuge, compense la composante du poids dans la direction du de l'axe du tube).
Cellule A5 : on entre 0 (t = 0)
Cellule B5 : =B1
Cellule C5 : =C1
Cellule D5 : =$D$1^2*B5-9,81*SIN($D$1*A5 + $F$2) (calcul de l'accélération à partir de l'équation différentielle)
Cellule A6 : =A5+$A$1
Cellule B6 : =SI(B5+C5*$A$1>$B$1;$B$1;SI(B5+C5*$A$1<$I$2;$I$2;B5+C5*$A$1)) (calcul de la position clampée à a ou à b si bille bloquée en butée)
Cellule C6 : =SI(OU(B5+C5*$A$1>$B$1;B5+C5*$A$1<$I$2); 0;C5+D5*$A$1) (calcul de la vitesse clampée à 0 si bille bloquée en butée)
Cellule D6 : =$D$1^2*B6-9,81*SIN($D$1*A6 + $F$2) (calcul de l'accélération à partir de l'équation différentielle)
On sélectionne les cellules de A6 jusque D6 et on les "tire" jusque la ligne 1005
Le graphique donne x en fonction de t
-----
On modifie à loisir les cellules contenant les valeurs de a, b , g, w, vo et xo pour visualiser les différents cas.
Voici un résultat :
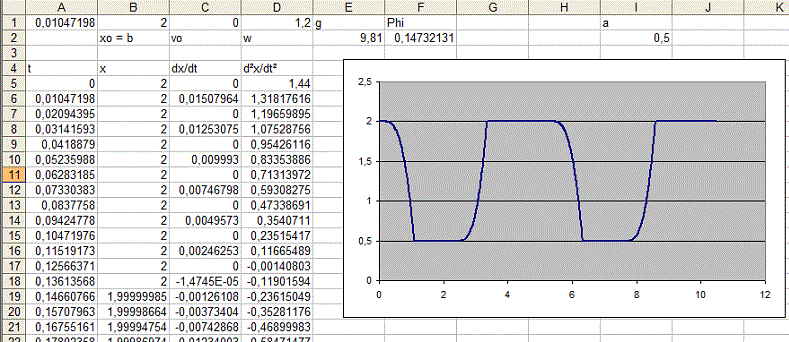
Il te reste à comprendre ce fichier Excel, toutes les réponses à tes questions s'y trouvent ...
entre autre comment "clamper" les positions de la bille aux extrémités du tube.

Bonjour à tous,
A mon tour d'être nouveau sur le site. Je me permets de rebondir sur cette discussion qui m'est très intéressante. Je suis actuellement en train de rédiger mon mémoire et j'aurais voulu avant tout remercier J-P pour sa lumière, vos réponses me sont très utiles, et j'aimerais savoir s'il était possible d'entrer personnellement en contact avec toi totorin?
J'essaie de mettre de l'ordre dans tout ce que vous avez dit et d'également tirer le tout sur Matlab. Si tu vois ce message pourrions nous entrer en contact afin que je te pose quelques questions? J'aimerais, si tu le veux bien, jeter un oeil sur ton code, des fois que tu l'aurais encore.
Bien merci