Inscription / Connexion Nouveau Sujet
vitesse angulaire d'un solide
Bonsoir,
J'ai une petite question à propos des vitesses angulaires de solides.
Si on considère une roue qui roule sans glissement sur le sol ainsi qu'un axe vertical rigide placée à une certaine distance de la roue.
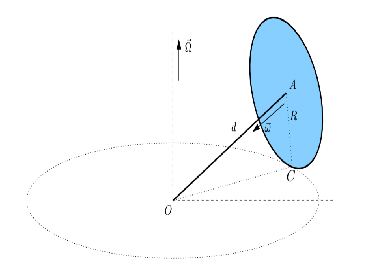
Il y a un autre axe rigide de longueur d qui relie le centre de la roue à l'extremité de l'axe vertical qui touche le sol (soit aussi l'origine du repère).
(voir schéma attaché au message)
On a donc deux vitesses angulaires dans ce problème : grand Omega et petit oméga.
Ma question est :
L'axe OA (qu'on considère comme un solide) a-t-il une vitesse angulaire grand Oméga, ou bien grand Oméga + petit oméga?
Merci beaucoup
Bonsoir,
Ton problème n'est pas paramétré avec suffisamment de précision que que l'on puisse répondre à ta question. L'angle au sommet A du triangle (OAC) vaut bien 90° je suppose ? Un vecteur rotation instantané caractérise la rotation d'un solide (ou d'un repère) par rapport à un autre solide (ou un autre repère) ; tes deux vecteurs rotations ne sont pas définis avec précision.
De façon générale, les vitesses angulaires ne s'ajoutent pas simplement quand les directions des vecteurs rotations sont différentes. La méthode pour obtenir la relation entre les deux vitesses angulaires consiste à exprimer la vitesse du point C puis à traduire en équation l'absence de glissement en C.
Merci de votre réponse,
En effet, l'angle OAC fait 90 degrés. L'axe rigide de longueur d est perpendiculaire au plan de la roue.
De ce que vous me proposez pour obtenir la relation entre les deux vecteurs, j'en comprends qu'il faut faire quelque chose du genre:
Oméga ( grand Oméga) oméga ( petit oméga)
Vc = Vo + Oméga cross OC
= Oméga cross OC
Vc = Vc + oméga cross CA
= oméga cross CA
On a donc Oméga cross OC = oméga cross CA
On tire d'ici déja que le sens de oméga doit être de A vers O.
Les deux produits vectoriels donne un vecteur qui n'a de composante que sur un axe z.
sin(Oméga,OC) = 1 , sin(oméga,CA) =1,
Donc : (Oméga*OC)/CA = oméga ?
sachant que OC peut être calculé avec pythagore et CA n'est autre que la rayon R
Mais si je voulais utiliser le point A et l'expression Va comme je l'ai fait pour Vc, lorsque je considère seulement le solide OA, on a:
Va = Vo + Oméga cross OA
ou bien Vo + (Oméga+oméga) cross OA.
Ce qui m'arrange et ce qui me permet de retomber sur ce le résultat précédant avec Vc est le premier choix. Mais concrètement, qu'est-ce qui me permet de ne pas compter petit oméga dans ce calcul.
Ceci a sûrement à voir avec la rotation instantanée et je serais ravi si vous pouviez m'expliquer cela.
Merci encore
De ce que je comprends de la figure, car je ne suis pas sûr de ce que tu appelles  et
et  ...
...
Je travaille dans un repère fixe par rapport au sol.
Condition de roulement sans glissement en C :
Résultat donné sous réserve dans la mesure où les vecteur rotations ne sont pas définis avec suffisamment de précision...
Désolé ! Je viens de me rendre compte que je me suis trompé : j'ai oublié un terme dans l'expression de la vitesse de C par rapport au sol ! Accepte mes excuses et surtout oublie le message précédent !
Soit (R) le repère terrestre et (R') le repère mobile tournant à la vitesse angulaire  autour d'un axe vertical passant par O.
autour d'un axe vertical passant par O.
La vitesse relative de C dans le repère relatif (R') est la vitesse due à la rotation de la roue autour de son axe (OA) à la vitesse angulaire  :
:
La vitesse d'entraînement de C est la vitesse qu'aurait le point C dans (R) en supposant  =0 :
=0 :
La vitesse de C dans (R) est la somme de ces deux vecteurs :
La condition de roulement sans glissement est donc :
Si on note D la distance OC :
la condition de roulement sans glissement conduit à :
L'axe d tourne à la vitesse de rotation autour de l'axe vertical
ET
tourne autour de son axe à la vitesse de rotation w
Si roulement sans glissement :
OC = RC(d²+R²)
circonférence du cercle de rayon OC : L1 = 2.Pi.RC(d²+R²)
Circonférence de la roue : L2 = 2Pi/R
Et donc w = L1/L2 .
Sauf distraction. 
La méthode de composition des vitesse n'est effectivement pas indispensable à l'obtention de la condition de roulement sans glissement. Elle n'est pas indispensable à l'obtention de l'expression de la vitesse de C par rapport au sol : Il suffit d'écrire la relation de distribution des vitesse dans un solide en considérant que la roue à pour vecteur rotation la somme des deux vecteurs rotation :
En revanche, la méthode que j'ai utilisée permet plus facilement, si cela est demandé ensuite, d'exprimer l'accélération du point C.


