Inscription / Connexion Nouveau Sujet
Vecteurs planeur
Bonsoir à tous,
Je suis actuellement en première S et je fais un TPE sur les planeurs.
Les deux matières concernées sont math et physique.
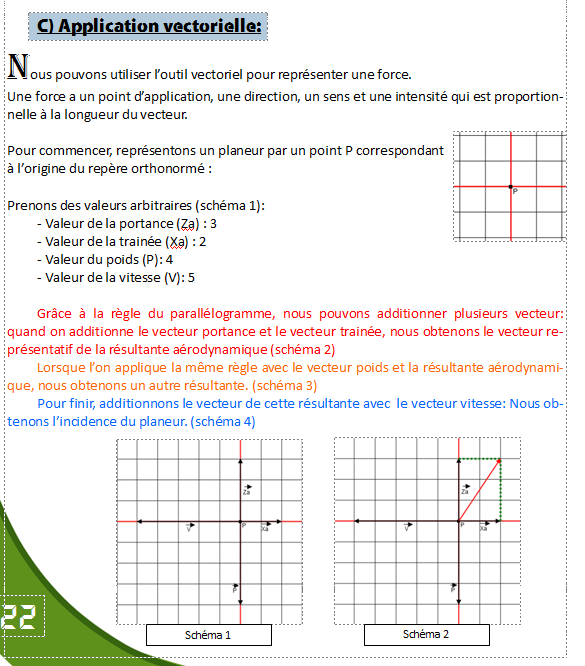
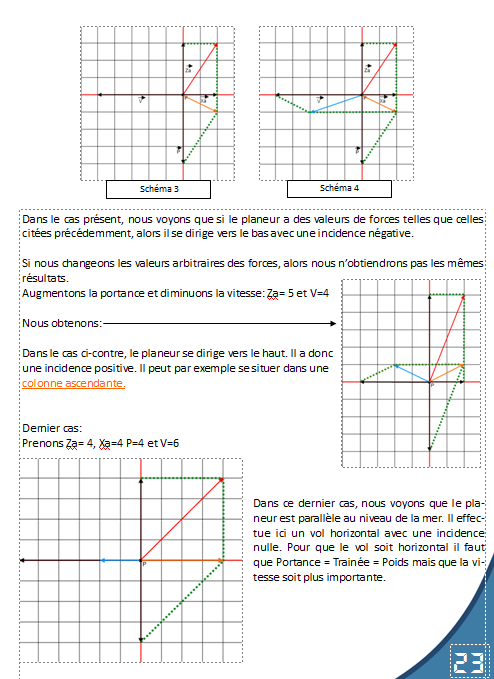
Pour la physique, aucun problème mais pour les maths, nous avons eu un peu de mal à en intégrer. Nous avons tout de même décider de mettre une application vectorielle des forces du planeur que voici (double page jointe).
Le problème qui s'impose est que la vitesse n'est pas une force ce qui rend notre application fausse (addition des vecteurs impossible)! Comment faire? Quelle est la force tirant le planeur en sachant que ce dernier n'a pas de moteur?
Si vous avez des réponses, des suggestions (car il est vrai que c'est un peu "simplet" pour des TPE de première S niveau math) ou des idées, n'hésitez pas!
Merci d'avance! 
Edit Coll : forum modifié
Bonjour,
Je ne sais pas où vous avez trouvé ces "explications" mais elles sont totalement farfelues.
La vitesse, en effet, n'est pas une force.
Sa direction est importante car elle indique (la tangente à) la trajectoire.
Quelques indications :
. la "pente" est définie par l'angle entre l'horizontale et la trajectoire du planeur (direction du vent relatif)
. l'"incidence" est définie par l'angle entre l'axe longitudinal du planeur et sa trajectoire (direction du vent relatif)
. l'"assiette" est définie par l'angle entre l'axe longitudinal du planeur et l'horizontale
La portance est toujours perpendiculaire à la trajectoire (direction du vent relatif)
La trainée est toujours parallèle à la trajectoire (opposée au vecteur vitesse)
Le poids est dans tout cela la seule force de direction et sens constants : la verticale et vers le bas.
En vol plané, en air calme :
. la composante du poids parallèle à la vitesse est égale et opposée à la trainée
. la composante du poids perpendiculaire à la vitesse est égale et opposée à la portance
Je pense qu'il ne manque pas sur le Web de sites de clubs de vol à voile qui proposent des notions théoriques correctes.

Merci de votre réponse!
Il est vrai que cela est un peu farfelue....
Mais si l'on décompose les forces du planeur il y en a donc uniquement 3:
La portance, le poids et la traînée. Comment se fait-il que le planeur avance sans force opposée à la traînée? Il est vrai que si l'incidence est négative, le planeur descendra et gagnera de la vitesse grâce à son poids mais je ne vois pas comment l'expliquer avec la présence d'une force.
Je ne sais pas si vous comprenez mon problème...
J'ai trouvé ce schéma sur internet qui résoudrait peut être mon problème:
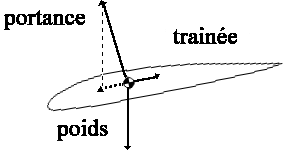
Mais quand le planeur a une incidence positive, il peut avancer quand même s'il dispose d'assez de vitesse. Donc ce schéma ne correspondrait plus..?
Source: http://scherrer.pagesperso-orange.fr/matthieu/aero/aerodyn.html
Ce schéma est assez correct.
Dans un vol stabilisé, un planeur est toujours en descente. Il peut être en descente dans un air qui monte (par exemple dans le cas de rues de nuages) et que le bilan soit qu'il monte par rapport au sol (mais il descend par rapport à la masse d'air).
Si la composante du poids parallèle à la vitesse est égale à la traînée ces deux forces ont une somme vectorielle nulle et, selon la première loi de Newton, le mouvement est rectiligne et uniforme ; la vitesse est donc constante (il ne faut pas dire "gagnera de la vitesse").
Quand à la portance elle est égale et opposée à la composante du poids perpendiculaire à la vitesse (dans le schéma que tu donnes, la longueur du vecteur représentant la portance est trop grande).

Les vecteurs représentant les forces dans le cas du vol plané d'un planeur (ou du vol plané d'un avion moteur arrêté)
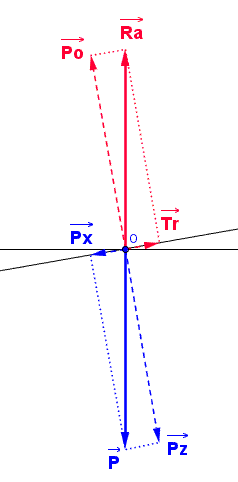
est le poids
est la résultante aérodynamique, strictement égale et opposée au poids
est la composante de la résultante aérodynamique perpendiculaire à la trajectoire : c'est la portance
est la composante de la résultante aérodynamique parallèle à la trajectoire : c'est la traînée
est la composante du poids parallèle à la trajectoire : c'est ce qui fait office de "moteur"
est la composante du poids perpendiculaire à la trajectoire.
Cette figure convient assez bien pour un avion moteur arrêté.
Pour un planeur il faudrait diviser par 10 environ l'angle de plané : au lieu de 10° prendre un angle d'environ 1° (ou même moins pour un planeur de performance moderne)
Les rapports suivants sont égaux :
Cz et Cx sont les coefficients aérodynamiques de portance et de traînée
Vsol est la vitesse par rapport au sol (sans vent)
Vz est la vitesse de chute verticale
D est la distance parcourue (sans vent) pour une perte d'altitude de h
 est l'angle de plané, angle entre la trajectoire et l'horizontale
est l'angle de plané, angle entre la trajectoire et l'horizontale
Pour des planeurs modernes ces rapports valent environ 40 ; 50 à 60 pour des planeurs de très haute performance !

Ouah, énorme, merci beaucoup de ton explication, tu as du y passer du temps en plus!
Encore Merci Coll, ça fait plaisir de voir qu'il y en a qui sont toujours prêt à aider les autres! 


