Inscription / Connexion Nouveau Sujet
Vecteur vitesse de rotation
Salut tout le monde,
S'il vous plait j'ai besoin d'aide dans l'exercice suivant (extrait Mine MP Physique 1 2014):
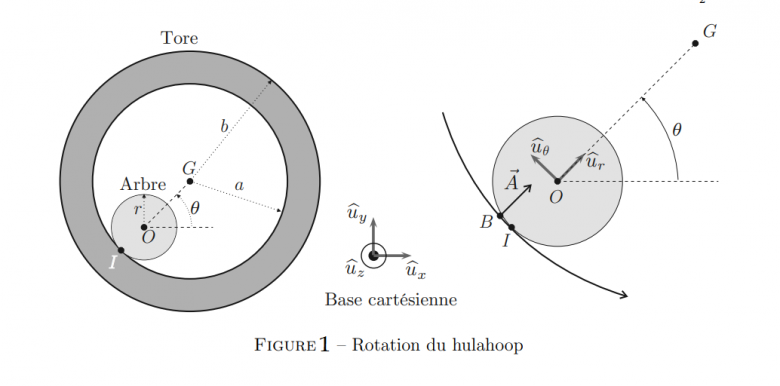
Considérons un tore de section rectangulaire en rotation autour d'un arbre cylindrique fixe et vertical, d'axe (O,z) et de rayon r, dans le référentiel terrestre supposé galiléen R0 .on note ∆=(G,z) l'axe de symétrie du tore, qui reste parallèle à (O,z). On note J le moment d'inertie du tore par rapport à (G,z), et M sa masse (Voir figure 1).
Le contact entre la paroi intérieure du tore et le cylindre vertical se répartit sur un segment vertical dont on note I le milieu . Il y a roulement sans glissement entre les deux solides. On note f le coefficient de frottement statique au niveau de ce contact.  est le vecteur vitesse angulaire de rotation du tore autour de son axe ∆. La position de G est repérée par l'angle
est le vecteur vitesse angulaire de rotation du tore autour de son axe ∆. La position de G est repérée par l'angle  .
.
Question :Établir la relation entre Établir la relation entre  et Q associée a l'hypothèse de roulement.
et Q associée a l'hypothèse de roulement.
D'après la correction : On a roulement sans glissement, donc :
 (I
(I Tore/R0)=
Tore/R0)= (I
(I arbre/R0)=0 ( car l'arbre est fixe dans R0 )
arbre/R0)=0 ( car l'arbre est fixe dans R0 )
Or :  (I
(I Tore/R0)=
Tore/R0)= (G/R0) +
(G/R0) + 
 GI
GI
Ce que je n'ai pas compris, c'est que d'après l'énoncé,  est le vecteur vitesse angulaire de rotation du tore autour de son axe ∆ et non pas autour de l'arbre cylindrique fixe dans R ! , et puisque l'axe ∆ est aussi en mouvement dans R, la vitesse de rotation du tore autour de l'arbre est obtenu par composition : la vitesse de rotation du tore autour de ∆ + la vitesse de rotation du ∆ autour de R, c'est à dire:
est le vecteur vitesse angulaire de rotation du tore autour de son axe ∆ et non pas autour de l'arbre cylindrique fixe dans R ! , et puisque l'axe ∆ est aussi en mouvement dans R, la vitesse de rotation du tore autour de l'arbre est obtenu par composition : la vitesse de rotation du tore autour de ∆ + la vitesse de rotation du ∆ autour de R, c'est à dire:  +
+ '.uz. donc on peut pas écrire :
'.uz. donc on peut pas écrire :
 (I
(I Tore/R0)=
Tore/R0)= (G/R0) +
(G/R0) + 
 GI
GI
car 

 (tore/R0)=
(tore/R0)= +
+ '.uz
'.uz
Donc on doit plutot écrire :
 (I
(I Tore/R0)=
Tore/R0)= (G/R0) + (
(G/R0) + ( +
+ '.uz)
'.uz) GI
GI
Ce qui m'a poussé a poser cette question, c'est que dans la question suivante, ils nous demande de calculer l'énergie cinétique du Tore. Puisqu'il est en rotation autour d'un axe ∆ de position non fixe ( mais de direction fixe) on utilise alors le théorème de Koenig : Ec= 1/2.m. (G)²+Ec*, avec Ec*=1/2. J.
(G)²+Ec*, avec Ec*=1/2. J.  (tore/R*) ²
(tore/R*) ²
Or d'apprès le corrigé : Ec*=1/2.J. ²
²
donc  =
= (tore/R*) !
(tore/R*) !
Excuser moi je suis un peu déroutant  :?
:?
Merci infiniment pour vos efforts
Bonjour,
Dans le référentiel lié au cylindre, la loi montre bien que pour un solide la vitesse d'un point est variable alors que la vitesse de rotation est la même pour tous les points.
Disons que le texte est maladroit, le tore tourne autour de I.
On a donc bien , les deux vitesses v(M) et v(G) sont bien évaluées dans R0.
Pour ce qui est du théorème de Koenig, le référentiel barycentrique est par définition en translation, donc
Le théorème de Koenig ne dépend pas de "en rotation autour d'un axe ∆ de position non fixe ( mais de direction fixe)".


