Bonjour,
je crois que tu confonds deux choses :
1° :  la notion de vecteur (vecteur vitesse, vecteur accélération, vecteur moment cinétique....) qui dépend du référentiel dans le quel on le calcule. Exemple : le vecteur vitesse d'un point à un instant donné n'est pas le même selon que tu l'exprimes dans un repère fixe par rapport à la terre ou dans un repère fixe par rapport au soleil. Par exemple, pour un point M quelconque :
2° : le même vecteur peut au même instant avoir des expressions différentes selon la base dans  laquelle tu le calcules. Ainsi, la vitesse d'un même point M par rapport à un même repère peut avoir des expressions différentes dans une base cartésienne et dans une base polaire.
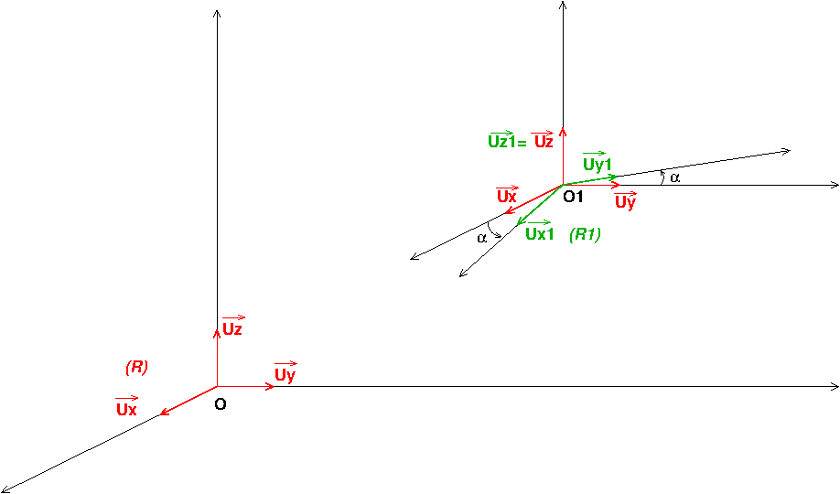
Concrètement ici, le vecteur    ne dépend que de la nature du mouvement de (R1) par rapport à (R) mais peut avoir des expressions différentes en fonction de la base dans laquelle tu l'exprimes. Cependant, l'expression peut aussi être la même, tout dépend des bases choisies ! Dans l'exemple correspondant au schéma ci-dessous, on peut poser :

Si, dans (R1), tu définis une base polaire : , le vecteur rotation a la même expression dans les deux bases puisque le vecteur unitaire Uz est commun au deux bases...

Voici le schéma :

Ah ok!!
Ce vecteur n'est pas comme les vecteur vitesses,accélérations...
En fait le mouvement de R1 par rapport à R reste le même,mais comme tu dis suivant la base dans laquelle on exprime la vitesse,si la base de projection est la même que celle de dérivation ou pas.
Mais en gros,même quand ce vecteur a des expressions différente suivant la base,ces expressions sont "égale" si j'ose dire non?

Ton schéma est très parlant en tout cas,merci pour ton aide .

Bonsoir,
Je crois que tu as compris !