Inscription / Connexion Nouveau Sujet
Vecteur en coordonnées polaires
Bonjour, je suis actuellement en L1 de Chimie, et j'ai une matière qui est la mécanique. Jusqu'à présent ça allait, mais cette après midi, en cours on à fait un exercice, et du début à la fin j'ai absolument rien compris. J'aimerai si possible que vous m'expliquer pour chacune des questions comment il faut faire.
Merci d'avance.
Voici l'exercice:
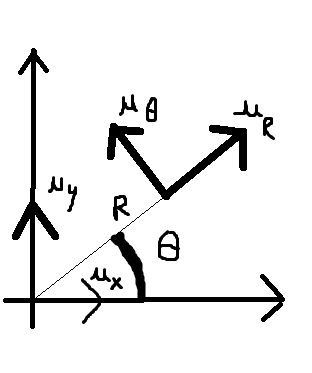
Soi(O,vecteur Ux,vecteur Uy) le repère cartésien de l'espace limité au plan xOy et vecteur Ur et vecteur Utéta les vecteurs unitaires de la base polaire en direction radiale et orthoradiale (voir figure).
1) Démontrer que les coordonnées cartésienne sont données en fonction des coordonnées polaires à travers les relations
x=r costéta et y=rsintéta
et que pour les vecteur unitaires on trouve
Vecteur Ur= costéta*vecteur Ux+sintéta vecteur Uy.
2) Calculer les dérivées de ces vecteurs unitaires, d'abord par rapport à l'angle téta, puis par rapport au temps.
3)Calculer à partir du vecteur position vecteur r(t)=r(t)*vecteur Ur les vecteurs vitesse vecteur point r(t) et accélération vecteur deux point r(t). (les points sont au dessus du "r", il signifie la dérivation).
4) Calculer la projection du vecteur c=3x*vecteur Ux+2y*vecteur Uy sur la direction radiale donnée par le vecteur unitaire vecteur Ur.
pour la question 1), il suffit de faire une projection des axes en coordonnées cartésiennes (x,y,z) sur ceux en coordonnées polaires (er,eθ,ez) -> il y aura donc forcément des angles en fonction de cosθ et sinθ qui interviendront
pour la question 2), il suffit de dériver par rapport au temps, c'est pas trop dur normalement.
pour la question 3), même raisonnement, tu dérives par rapport au temps ton vecteur position pour trouver vitesse et accélération :
tu as donc =r .
en dérivant tu obtiens la vitesse : v() = dr/dt .
+ rdθ/dt .
etc pour l'accélération


