Bonjour
Tu mets R+h en facteur dans la 1ere racine (au dénominateur)
Et comme h/(R+h) est très petit tu fais un développement limité pour simplifier l expression

Oui, un DL, mais alors il me semble qu'il y a un erreur d'un facteur 2.

... Ou bien une erreur (oubli d'une racine carrée) dans la formule réponse de l'enoncé.


La vitesse d'un satellite de masse m à l'altitude h autour d'un astre de rayon R et de masse M  est

La quantité de mouvement de ce satellite est

Si on fait passer h à h + h, la quantité de mouvement du satellite devient :

La différence de quantité de mouvement pour changer d'altitude est










Sauf distraction.  

Bonjour

Merci beaucoup pour ces réponses

Je pense effectivement que la racine carrée a été oubliée, je trouve le même résultat

Je ne vois pas vraiment l'utilité de cette simplification, sauf avoir les variables qui ne reviennent qu'une seule fois :
On ne pouvait pas directement passer à l application numérique ?

Merci encore

Belle journée

Le terme entre parenthèses se simplifie nettement si on fait
Un D.L.

Bonsoir,

Le DL à utiliser est (1+x)ⁿ = 1 + nx (ici n = -0.5) ?

(DL en 0 à l'ordre 1 avec f(0) = 1 et f'(0) * x = -0.5 (0 + 1)^-1.5 x = -0.5x)

On a donc

Cela correspond à la variation de vitesse (sans le "m" devant pour éloigner le satellite de la Terre

Cela voidrait dire que pour éloigner la satellite , il faut diminuer sa vitesee : est-ce cohérant ?

MErci encore

Bonne soirée

Bonsoir
Je te rassure: il faut bien fournir de l énergie pour que le satellite monte (et augmenter à certains moments sa vitesse durant la manœuvre)
Mais en fin de manoeuvre, sur sa nouvelle orbite à 610km de haut , il aura une vitesse plus faible car il est plus haut (sur une orbite circulaire ) tandis que l'Ep et l'Em auront, elles, augmenté

OK pour le DL ...

Mais, pour moi, ce n'était pas ce qui était attendu dans la question initiale.

Il y avait une erreur dans la formule indiquée dans le post initial ... (pour moi, il manquait une racine carrée).

Un DL n'amène pas une "formule" qui ressemble un tant soit peu à celle de l'énoncé initial.

De plus, il faut se méfier d'un DL (surtout du premier ordre).

Il n'y a guère de problème de précision avec l'application numérique de l'énoncé, mais garder cette simplification pour d'autres valeurs numériques pourrait bien être hasardeux.(il resterait à donner des critères pour la précision)

A remarqer que les données numériques de l'énoncé sont loufoques, un satellite de la Terre à 600 m d'altitude est une absurdité.

En tout cas, oublier la formule simplifiée, par exemple si on veut faire passer un satellite d'une orbite proche de la Terre (quelques centaines de km) à une orbite géostationnaire ... ou autre chose du même accabit.

Ce n'est bien sûr que mon avis.

Bonsoir,

merci pour vos réponses !

Oui je pense aussi que la racine s'est envolée en prenant la correction

Un DL d'un ordre supérieur (qui simplifie nettement moins la formule) serait plus judicieux pour la précision du résultat ?

On a considéré que --> 0 pour le DL, c'est cela (plus le ) la source d'imprécisions  ?

Pour les données, erreur de lecture de ma part, elles sont en km

Merci encore !

Bonne soirée !

Un DL du 1er ordre simplifie (un peu) la relation.

Un DL d'ordre plus élevé risque bien d'être aussi (voir plus) long à écrire que la relation exacte.

Un DL amène toujours de l'imprécision ... on est donc censé evaluer à chaque fois si celle-ci est compatible avec ce qu'on veut faire de la réponse trouvée... Et c'est là que souvent cela foire, on oublie de le faire (ou on ne sait pas comment s'y prendre).

On dit "parce que ceci est petit devant cela", oui, mais encore ?
Cela donne quoi comme ordre de grandeur de l'erreur ?

C'est un peu pareil partout, on tente de donner des relations simples, facile à manipuler ... mais on oublie, quand on les utilise, les restrictions éventuelles à appliquer.

On voit ceci, dans plein de domaines, par exemple en optique, où plein de "lois" ont été établies sous certaines conditions (taille de l'objet petite par rapport la distance focale, ou épaisseur supposée quasi nulle ou  ...)

Et puis, on applique ces mêmes lois en oubliant ces restrictions (c'est un grand classique).

Attention, je ne prône pas le non usage des lois simplifiées (par des DL ou autrement), elles sont presque indispensables si on ne veut pas complexifier outrageusement la réflexions sur certains problèmes ...  

Mais attention aux pièges que cela entraîne.

Bonsoir,

merci pour votre réponse

En effet, nous n'avons jamais abordé l'évaluation de la précision d'un DL

L'ordre de grandeur de est 10^-3

Cela signifie que la précision du DL, donc du résultat est de 0.1% ?

Faut-il considérer cela de la meme sorte qu'une incertitude U_b ?

Il est vrai que cette année on a utilisé beaucoup d'approximations en optique et mécanique (sin(x)   pour les petits angles par exemple) sans jamais discuter de la précision

Merci encore,

bonne soirée

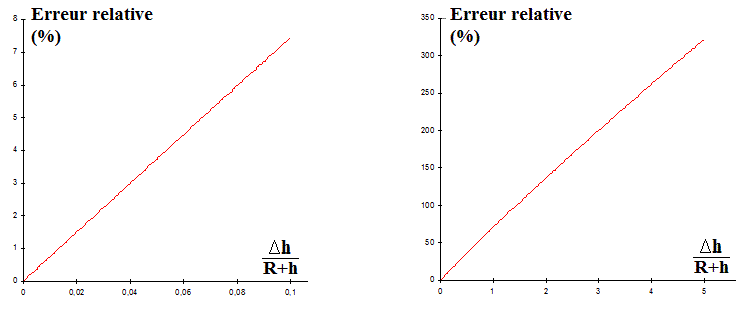
D'où l'obligation impérieuse de ne pas oublier les conditions sous lesquelles une formule approchée a été établie.

Si on commet la bêtise de l'utiliser hors de ces conditions (par exemple ici pour faire passer un satellite d'une orbite basse à une orbite géostationnaire ... alors plus de 300 % d'erreur.)

Merci beaucoup pour ces précisions qui aident à se souvenir des 'conditions' avant d'utiliser une loi ou de faire une approximation/simplification

Le graphe tracé correspond à pour avoir la précision en % ?

(Je suis également intéressé par le logiciel qui permet de tracer ces graphes )

Merci encore !

Bonne soirée

Erreur relative sur le calcul de Delta p (qui est ce qui était demandé):

Erreur(en %)

Avec :

la valeur de calculée par la formule exacte.
la valeur de calculée par la formule utilisant le DL.