Inscription / Connexion Nouveau Sujet
Valeur moyenne de divers signaux
Bonsoir,
Je fais un exercice pour m'entrainer et je rencontre des difficultés. J'aimerai de l'aide s'il vous plait.
Voici l'énoncé :
1) Calculer la valeur moyenne d'un signal c(t) de période T valant Cm sur l'intervalle [0, T/2] et 0 le restant de la période.
Pour cela, j'ai appliqué la formule de la valeur moyenne : <c(t)> = 1/T * l'integrale de 0 à T/2 c(t) dt. Ensuite j'ai exprimé c(t) en fonction de cm ce qui me donne : c(t) = Cm cos(wt+ phi) et puis j'ai trouvé une primitive de c(t) mais après je ne sais pas comment continuer, je ne sais pas si j'ai bien commencé.
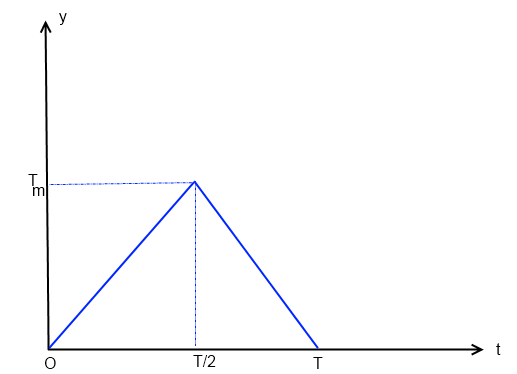
2) Reprendre le calcul pour le signal de forme triangulaire Tri(t) valant 0 au début de la période, croissant jusqu'a Tm de 0 à T/2 et décroissant jusqu'a 0 ensuite. Je ne comprends pas la question.
3) Pour un signal sinusoidal quelconque, donc d'expression s(t)=Sm cos(wt+phi), quelle est la valeur moyenne?
je ne sais pas comment on calcule la valeur moyenne, je connais la formule mais je ne sais pas l'appliquer.
Merci d'avance.
Bonjour,
Pour le calcul de la moyenne, l'intégrale va de 0 à T. Ou plus généralement de t0 à t0+T.
Pour la première question, dans le texte, tu dis d'abord que c(t)=Cm. Ensuite, tu y mets un cosinus. Où est le vrai?
bonsoir,
oT c(t) dt
1) la fonction à intégrer est:
c(t) = Cm sur [O,T/2]
c(t) = 0 sur ]T/2,T]
donc oT/2 Cm dt + T/2T 0 dt ) = ...
2) la fonction à intégrer est:
c(t) = 2Tm t/T sur [O,T/2]
c(t) = 2Tm(1 - t/T) sur ]T/2,T]
3) c(t)=Sm cos(wt+phi),
Merci à vous de m'avoir répondu.
sanantonio312 : Effectivement, je n'ai pas réussi à interpréter les éléments de l'énoncé correctement.
krinn : Pour la question 2), comment est-ce que vous etes parvenu à exprimer c(t) de cette manière?
et pour la question 3), dois-je juste exprimer la valeur moyenne ou dois-je la calculer?
dois-je juste exprimer la valeur moyenne ou dois-je la calculer?
il faut calculer les valeurs moyennes sinon c'est pas drôle
D'accord, merci beaucoup, mais je n'aurais jamais trouvé ça tout seul!
Et comment est-ce qu'on calcule les valeurs moyennes justement? Je sais qu'il faut trouver la primitive etc enfin, je vois comment calculer une intégrale, mais je ne sais pas avec quelle donnée numérique je peux remplacer chaque terme.
c'est un simple calcul intégral
par ex.
1) oT/2 Cm dt + T/2T 0 dt ) = 1/T [Cm t] oT/2 + 0
= 1/T CmT/2 = Cm / 2
) ou cos(wt+
Annuler
connectez vous