Inscription / Connexion Nouveau Sujet
Une question de méthode ....
Bonjour,
Je suis dans un problème de physique.
L'énoncé est le suivant :
Une sphère conductrice de centre 0 de rayon R porte une densité  uniforme. Dans le référentiel du laboratoire, elle tourne à vitesse angulaire
uniforme. Dans le référentiel du laboratoire, elle tourne à vitesse angulaire  constante.
constante.
Dans une partie on nous dit :
On admet qu'un dipôle magnétique de moment magnétique placé en O crée en un point P tel que
=
un champ magnétique pour lequel le potentiel-vecteur s'écrit
(P) = µo/(4pi) *

/r3
On donne l'expression en coordonnées sphériques du rotationnel.
a. Exprimer le potentiel-vecteur créé en un point P par le dipôle magnétique dans la base locale des coordonnées sphériques en supposant que = M *
b. En déduire le champ magnétique créé en P par le d^pôle mégnétique.
___________________________________________________________________________________
Merci de m'expliquer comment faire ces deux questions 
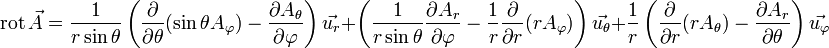
Bonsoir,
Il y a un truc qui me paraît bizarre...
Mais, si et
, on a :
Et là, j'ai un problème  ...
...
sauf erreur de ma part...
Apparemment, on trouve ...
La question b, c'est et on aurait le plaisir d'utiliser le rotationnel en coordonnées spériques mais si
...


