Inscription / Connexion Nouveau Sujet
Une barre qui oscille
Bonjour, encore un exercice dont je comprends pas bien la résolution,
Une barre homogène de longueur finie et de masse M est posée sur deux cylindres tournant en sens opposé. Les axes des deux cylindres sont distant de 2l, le coefficient de frottement (dynamique) entre la barre et les cylindres est µ. On supposera qu'il y toujours un glissement entre la barre et les cylindres (par exemple en appliquant une très grande vitesse de rotation aux deux cylindres).
a)La barre est posée de telle sorte que son centre de masse est à une distance x0 de la
médiatrice du segment de droite qui joint les deux axes. Montrer que le mouvement
de la barre une fois posée est sinusoïdal de pulsation
b) Que se passe-t-il si on refait la même expérience en inversant le sens de rotation des
deux cylindres ?
Aide : Faire un bilan des forces et des moments sur la barre lorsque celle ci est à
une position quelconque x par rapport à la médiatrice du segment de droite qui joint les
deux axes. Appliquez ensuite la relation fondamentale de la dynamique et le théorème du moment cinétique.
Je ne comprends pas pourquoi on nous conseille de faire un bilan des moments, et je ne comprends pas par rapport à quel axe appliqué le théorème du moment cinétique ?
Bonjour
Il faut commencer par faire un schéma bien propre en faisant bien attention aux sens des réactions tangentielles .
Je te laisse réfléchir et proposer une solution.
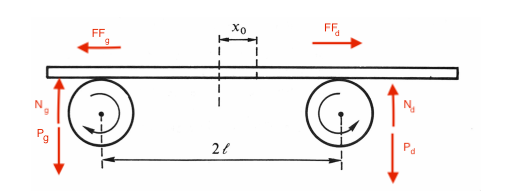
Pour être honnête je ne comprends même pas comment il peut y avoir un oscillement, je m'explique,
la barre étant homogène le poids à gauche< poids à droite => Ng<Nd
donc la force de frottement(FF) FFg<FFd à ce moment la barre avance vers la gauche mais lorsque x0=0; FFg=FFd, les forces à droites et à gauche étant identique la barre ne devrait pas bouger
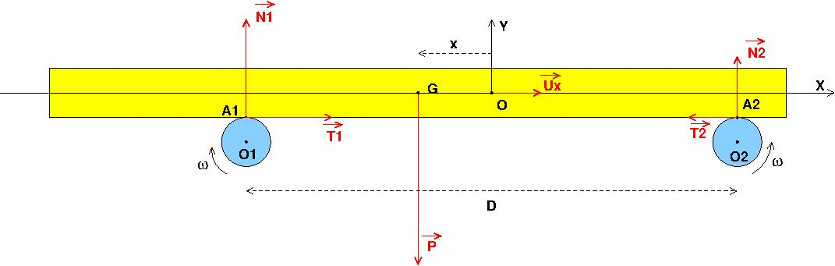
Voici un schéma plus précis qui t'aidera peut-être. Le système étudié est la barre seule (en jaune) Le repère d'étude, fixe par rapport à la terre est (O,x,y) tel que l'axe vertical (Oy) soit équidistant des deux axes de rotation des cylindres.
Compte tenu des sens de rotation des deux cylindres et de la valeur de la vitesse angulaire de rotation  relativement élevée, les actions tangentielles
relativement élevée, les actions tangentielles et
des deux cylindres sur la barre sont toujours orientées vers l'origine O du repère.
L'étude qualitative est assez simple : Quand G est à gauche de O (cas de la figure, x<0), N1>N2 donc, d'après la loi de coulomb sur les frottements sec T1>T2 donc le vecteur est orienté vers O.
Quand G est à droite de O, il faut inverser les sens des inégalité de sorte de le vecteur
a changé de sens et donc, est encore orienté vers O. Conclusion :
constitue une force de rappel qui tend constamment à ramener G vers O, un peu comme le ferait un ressort. Il y a donc oscillation compte tenu des conditions initiales.
Je te laisse mettre tout cela en équation. L'idée consiste à montrer :
puis à appliquer à la barre la relation fondamentale de la dynamique.
Deux remarques :
* tu dois connaître la loi de Coulomb sur les frottements solides ;
* tu vas être amené à appliquer à la tige le théorème du moment cinétique en G ; pour arriver au résultat simple attendu par l'énoncé, il faut supposer la barre très longue devant son épaisseur ce qui permet de considérer les points O, G, A1 et A2 comme pratiquement alignés horizontalement.
Je te laisse travailler.