Inscription / Connexion Nouveau Sujet
Un problème de physique avec un skieur et une bosse
Bonsoir, j'aurais besoin de votre aide pour un problème que je n'arrive vraiment pas à résoudre. merci d'avance pour votre soutiens.
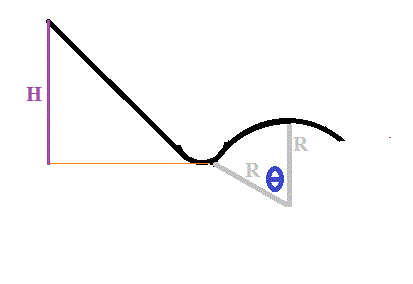
Un skieur de masse m descend le long d'une piste, sans frottement. A la fin de la piste se trouve une bosse, dont le rayon de courbure est R. Le point d'inflexion où la courbure de la piste se raccroche à la courbure de la bosse se trouve à un angle θ par rapport à la verticale (cf. figure). En supposant que le skieur d ́ebute sa course folle à partir d'une hauteur H sans vitesse initiale, répondez aux questions suivantes:
a) Quelle est la hauteur minimale pour H afin que le skieur ne soit pas obligé de défaire ses skis et de monter la bosse à pied ?
b) Quelle est le poids du skieur dans son propre référentiel lorsqu'il traverse le plus haut point de la bosse?
c) A quel point et à quelle vitesse le skieur décolle-t-il? 
Ps: je n'arrive pas à insérer la figure mais c'est une simple courbe à une bosse.
Merci beaucoup !
a)
E cinétique du skieur au départ : Ec1 = 0
E potentielle de pesanteur du skieur au départ : Epp1 = mgH (avec le bas de la pente comme niveau référence pour les Epp nulles)
E mécanique du skieur au départ : Em1 = Ec1 + Epp1 = mgH
E potentielle de pesanteur du skieur au sommet de la bosse : Epp2 = mgR.(1 - cos(theta))
Pour que le skieur puisse franchir la bosse sans monter à pied, il faut :
Epp2 <= Em1
mgR.(1 - cos(theta)) <= mgH
H >= R.(1 - cos(theta))
-----
b)
Conservation de l'énergie mécanique (puisque supposé sans frottement) --->
mgH = mgR.(1 - cos(theta)) + (1/2).mV² (avec V la vitesse du skieur au point haut de la bosse)
gH = gR.(1 - cos(theta)) + (1/2).V²
v² = 2gH - 2gR.(1 - cos(theta))
Force centrifuge sur le skieur au sommet de la bosse :
Fc = mv²/R
Fc = m.[2gH - 2gR.(1 - cos(theta))]/R
Cette force est verticale vers le haut.
Dans un référentiel lié au skieur :
P = mg - Fc (vertical vers le bas)
P = mg - m.[2gH - 2gR.(1 - cos(theta))]/R
P = mg - 2mgH/R + 2mg.(1 - cos(theta))
P = mg.[3 - 2H/R - 2.cos(theta)] ... sous évidemment la condition H >= R.(1 - cos(theta))
-----
c)
Calculer (en fonction de la position du skieur) la composante de son poids normale à la piste (de la bosse)
Calculer la force cenrifuge sur le skieur (en fonction de la position du skieur)
Le skieur décolle au point où la F centrifude devient > la composante du poids normale à la piste.
...
Question: la bosse reste t-elle avec le même rayon de courbure plus loin que le sommet de la bosse ?
-----
Sauf distraction.