Inscription / Connexion Nouveau Sujet
Turbines hydrauliques
Bonjour à tous !! 
Je suis actuellement étudiant en énergies renouvelables et j'aurais besoin de renseignements pour mes préparations de TP...
Je n'ai eu que très peu de cours sur les turbines donc j'ai des difficultés à résoudre ce petit problème:
Données de l'énoncé:
Turbine Pelton ==> Vi(vitesse maximale entrée injecteur)= 140m/s pour une chute de hauteur de 1000m. (Calcul que j'ai effectué avec la formule Vi= 2gh)
2gh)
Si toute l'énergie de la chute est convertie en énergie de rotation de la turbine, quelle est cette énergie cinétique maximale ?
- Je n'arrive pas à mettre en relation la formule pour obtenir les 140m/s du dessus avec la relation de l'énergie de rotation K=1/2mv² (valeur de m?)
Montrer que le rendement de la turbine s'écrit en fonction de la vitesse de rotation de la roue Vr:
nu=(4Vr(Vi-Vr))/Vi²
NB: Le maximum de l'énergie cinétique de l'eau doit être transmis à la roue. La vitesse de l'eau à la sortie des augets doit donc être minimale.
A partir de la formule précédente, trouver la vitesse optimale de la roue Vr en fonction de la vitesse initiale du jet Vi pour obtenir le rendement maximal.
- Pour moi ici on isole Vr, on connait Vi et le rendement est de 1. Mais je trouve un résultat négatif...
Quel serait alors le rendement optimal ?
- Pour moi, ici on remplace la valeur de Vr obtenu à la question du dessus
Merci par avance pour vos réponses 
Bonsoir
Tu trouveras ici une démonstration des principales formules concernant la turbine Pelton :
![]()
A mon avis, la première question est mal posée. Connaître l'énergie cinétique de rotation de la turbine n'a pas d'intérêt. Ce qui est intéressant c'est la puissance mécanique que peut fournir la turbine au dispositif qu'elle entraîne : alternateur électrique par exemple. Il me semble plus pertinent de reformuler la question de la manière suivante : "quelle est la puissance maximale susceptible d'être fournie par la turbine ? " Cela revient à déterminer la puissance cinétique de l'eau : produit du débit massique de l'eau par l'énergie cinétique massique : . Bien sûr, la puissance réelle de la turbine est plus faible car l'eau sort de la turbine avec une énergie cinétique massique nettement plus faible que l'énergie cinétique massique entrante mais pas nulle.
D'accord ! Merci beaucoup pour les infos et le lien 
Si d'autres personnes ont des suggestions, notamment pour la démonstration du rendement ou autre, je suis preneur !
Salut,
nu=(4Vr(Vi-Vr))/Vi²
dnu/dVr = 4/Vi² * (Vi - 2.Vr)
dnu/dVr > 0 si Vr < Vi/2 --> nu est croissant
dnu/dVr = 0 si Vr = Vi/2
dnu/dVr < 0 si Vr > Vi/2 --> nu est décroissant
Et donc nu est max pour vr = Vi/2
nu(max) = (4*Vi/2 * (Vi-Vi/2))/Vi² = 2 * 1/2 = 1
Sauf distraction. 
Bonjour à tous,
Après avoir réalisé le TP sur les turbines, j'ai une petite question concernant la turbine Francis.
Je dois déterminer le rendement de la turbine en fonction de l'orientation des aubes directrices. Sauf que j'ai des rendements qui dépassent 100% d'où mon interrogation...
Je mets en pièce jointe les résultats obtenus.
Merci par avance pour votre aide 
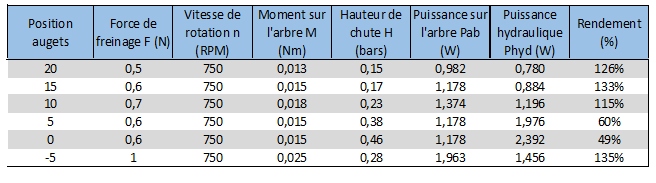
L'interrogation me semble légitime.
Ce type de turbine a un rendement max de l'ordre de 90 % ... et en tout cas jamais de plus de 100 %
On ne peut pas, à partir des chiffres du tableau, déterminer d'où viennent les erreurs, surtout sans précision sur la manière dont les essais ont été menés.
Elles peuvent venir de :
- les mesures de la force F
- la valeur prise en compte comme bras de levier pour calculer le Moment sur l'arbre.
- l'angle fait entre un rayon et la direction de la force F (qui n'est peut-être pas de 90°)
- la valeur du débit dans la turbine (qui influence les valeurs de la puissance hydraulique)
...
Sauf distraction. 
D'accord merci !
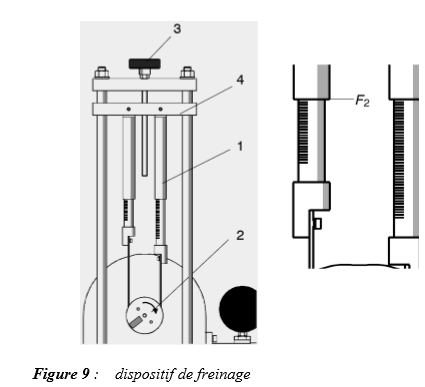
Les essais ont été fait avec le modèle HM 150-20 que j'ai mis en photo avec ce commentaire.
- Pour la force de freinage, nous trouvons les valeurs en calculant la différence des deux forces quand nous tournons le volant (3) en haut du dispositif. Dans notre cas, nous ne touchons pas à la vitesse de rotation donc la force de freinage est presque la même. Elle est de 1 à la fin car les aubes sont fermées donc l'arbre s'arrête de tourner. J'ai également mis la photo du dispositif.
-La vitesse de rotation ne varie pas car nous la maintenons à 760 tr/min.
- Le moment est calculé de la façon suivante:
M= F* (D/2) avec (D = 0,05 m)
- La hauteur de chute est lue sur la mano qui est sur le dispositif. Doit-on laisser cette valeur en bars ?
- La puissance sur l'arbre est égale = moment * (2 *n)/60) avec n=760 tr/min
*n)/60) avec n=760 tr/min
- La puissance hydraulique s'obtient en faisant Phyd=débit* eau*G*H avec débit = 0,00053 m3/s. Phyd=0,00053*1000*9,81*0,15
eau*G*H avec débit = 0,00053 m3/s. Phyd=0,00053*1000*9,81*0,15
Pour moi, je pense que l'erreur vient de l'unité de la hauteur de chute en bars mais je ne suis pas sûr.

1 bar correspond à une pression de 10,2 m d'eau
0,15 bar correspond à une pression de 1,53 m d'eau
Mais cela ne fera qu'augmenter l'erreur sur le rendement calculé si le débit est bien de 0,00053 m³/s
Pour 0,15 bar (1,53 m d'eau)
P hyd = 0,00053 * 1000 * 9,81 * 1,53 = 7,95 W
Donc il y a d'autres erreurs.
Vérifie si la force F lue n'est pas exprimée en kgf plutôt qu'en N.
Si c'était le cas, alors F = 0,5 kgf --> F = 4,905 N
Moment = 4,905 * 0,05/2 = 0,123 Nm
N = 760 * 2Pi/60 = 79,6 rad/s (ici aussi, il y a hésitation, il est éxrit 750 tr/min ou bien 760 tr/min ???)
P arbre = 0,123 * 79,6 = 9,79 W
Et rendement = 7,95/9,79 = 0,81 (81 %)
Mais cela fait évidemment beaucoup de "si" ...
A toi de vérifier si ce que j'avance comme possibilité est vrai ou non.
On peut encore discuter sur la précision ... lire une force (F) avec 1 chiffre significatif ne permet pas d'avoir une précison décente sur le calcul du rendement.



