La terre est assimilée à une sphère homogène de centre O et de rayon R. Soit g0 la valeur de
l'accélération de la pesanteur à la surface de la terre. On ne tient pas compte de la rotation de la
terre.
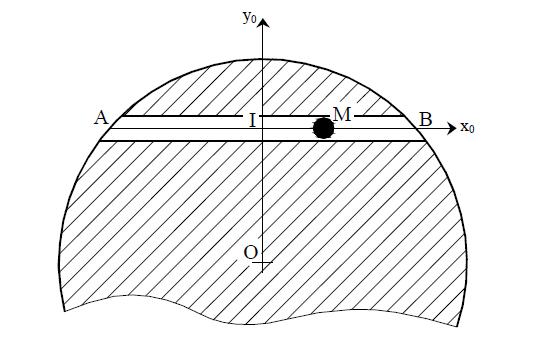
On relie deux villes A et B par un tunnel rectiligne de longueur d. Un train assimilable à un point
matériel M se déplace sans frottement dans le tunnel. On note r la distance OM.
Le référentiel terrestre ℜ0 est considéré comme galiléen ; il est rapporté au repère (I,x0,y0,z0)


2.1 Déterminer g l'accélération de la pesanteur au point M en fonction de g0, r et R.
2.2 Ecrire sous forme vectorielle le théorème de la résultante dynamique appliquée au point M.
2.3 En déduire l'équation du mouvement du point M.
2.4 Déterminer la période T du mouvement du point M. En déduire la durée tAB du trajet AB en
fonction de g0 et R.
2.5 Déterminer la vitesse maximale Vmax du train en fonction de d, g0 et R.

bon voila ce que j ai fait :
1) theoreme de gauss:

=g.ds
à la surface je trouve
=g₀*4R²

en un point M

= g₀*4 r²
le flux etant conserve on a g=g₀*R²/r²

2)PFD:
ma = P+R    (en vercteur)
mais la je bloque parce que quand je projette selon x₀ , je tombe sur une equation tres bizarre :s :s