Inscription / Connexion Nouveau Sujet
trombone de koenig
Bonjour.
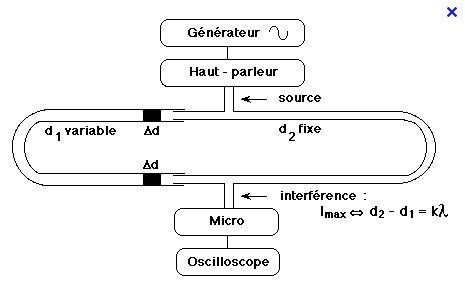
Le trombone de Koenig est un dispositif de laboratoire permettant de faire interférer deux ondes sonores ayant suivi des chemins différents. Le haut- parleur, alimenté par un générateur de basse fréquences, émet un son de fréquence f=1500 Hz . On mesure le signal à la sortie avec un microphone branché sur un oscilloscope . En déplaçant la partie mobile on fait varier l'amplitude du signal observé. Elle passe deux fois de suite par une valeur minimale lorsque l'on déplace d1 de d=11,5cm  2mm .
2mm .
Déterminer la valeur de ma célérité du son dans l'air à 20°C, température à laquelle l'expérience est faite .
je ne vois pas du tout comment commencer et je ne comprend pas l'histoire des deux valeur minimale de l'énoncé .
merci d'avance .
Bonsoir,
Que vaut la longueur d'onde d'après les informations de l'énoncé ?
On te donne la fréquence de l'onde. Tu en déduis facilement la célérité dans l'air à cette température de 20 °C

salut .
la longueur d'onde est 11,5 non ? car ils disent que lorsque l'on déplace de d1 de d=11,5 , l'onde passe deux fois de suite par une valeur minimale .
Quelle est la différence de marche entre les deux trajets quand la partie mobile est déplacée de d = 11,5 cm ?

On peut donc avoir une réponse svp ?
Et si on veut calculer l'incertitude relative de cette valeur on fait comment ?
donc je vois pas comment calculer cela .
la longueur d'onde j'ai dis que c'est 11,5 cm mais je comprend pas vraiment pourquoi c'est ça . parce que je comprend comment il peut y avoir 2 fois de suite une valeur minimale .
juste . est-ce que la différence de trajet va nous servir pour la vitesse ? car je ne vois pas pourquoi elle nous servirait .
La différence de marche entre les deux trajets est ce qui explique les interférences constructives et les interférences destructives, n'est-ce pas ? Alors...

Exact !
Que vaut donc la célérité du son dans l'air à la température de 20 °C, celle de l'expérience ?

En effet la longueur d'onde n'est pas 11,5 cm
De combien doit varier la différence de marche pour avoir deux minima successifs ?

23cm . donc lambda=23cm eet maintenant sa marche . on trouve 340 m/s.
mais qu'ils disent 2 minima de suite . sa veut dire que l'on a une valeur minimal puis que lorsque l'on déplace d1 de 11,5cm on a à nouveau un minima ? parce que je ne sais pas trop comment l'interpréter .
Oui c'est cela, à ceci près que je trouve v = 345 m.s-1
Oui, deux minima successifs signifie qu'en déplaçant la partie mobile on va observer de nombreux minima (un tous les 11,5 cm). Et que deux minima consécutifs sont séparés par un déplacement de la partie mobile de 11,5 cm


 Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 

 f . mais la je trouve : 172,5 m/s
f . mais la je trouve : 172,5 m/s
