Inscription / Connexion Nouveau Sujet
Travail - théhorème de l'energie cinétique
Bonjour 
Je n'arrive pas à déterminer l'expression de la Force motrice (tension du fil) et de la réaction dans le problème suivant :
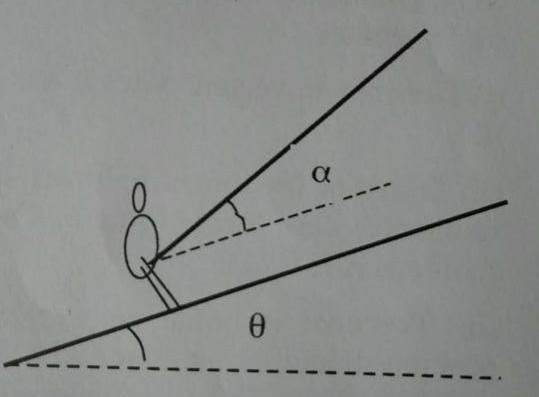
Skieur tiré par un remonte pente (angle a par rapport au sol penché : o = 30°)
Sol faisant un angle de 15° avec l'horizontale
Masse du skieur : 70kg
Longueur du voyage : 500m
Uc de la neige : 0.1
Je pensais simplifier en ne prenant qu'un angle total piste + remonte pente (a+o = 45°) mais cela ne mene à rien
Merci d'avance pour votre aide ! 
Bonne soirée
Bonjour,
Bonjour,
La réponse dépend de la nature du mouvement du skieur.
S'il s'agit ( comme c'est probable) d'un mouvement uniforme alors les données de l'énoncé permettent d'appliquer le théorème de l'énergie cinétique :
La variation d'énergie cinétique du skieur pendant un intervalle de temps est égale à la somme algébrique des travaux de toutes les forces qui s'exercent sur ce skieur pendant cet intervalle de temps.
Bonsoir,
tout d'abord merci pour votre réponse !
oui, oubli de ma part, vitesse constante de 5m/s
Le théorème de l'EC permet d'écrire que  Ec (=0 car v constante) = W(P) + W(R) + W (F) (Poids/réaction/force)
Ec (=0 car v constante) = W(P) + W(R) + W (F) (Poids/réaction/force)
d'où -mgL - T L + F L = 0
(T = réaction tangeantielle due aux frottement, la réaction normale ne travaillant pas)
je ne vois pas vraiment comment arriver à l'expression de la Force F et de la réaction avec cela
Nous avons le résultat de l'expression de F sans justification :
F = mg
Où a = angle alpha, o = angle téta, uc coefficient de friction ski/neige
Merci d'avance,
Bonne soirée
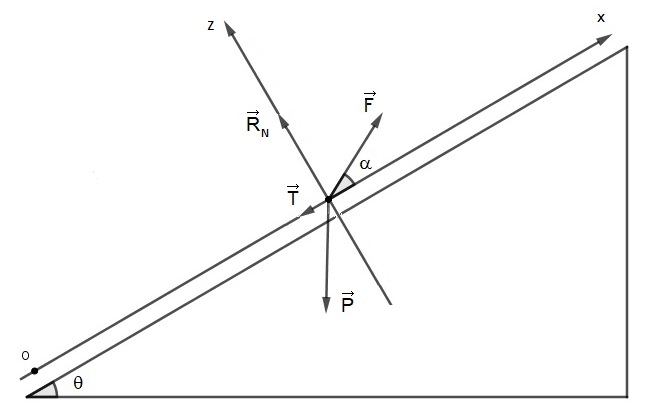
3 forces s'exercent sur le skieur :
Son poids , La force de traction
, la réaction du sol
peut être décomposée en
, perpendiculaire à la piste et
(frottements) parallèle à la piste.
Le principe d'inertie donne :
La projection de cette équation sur un axe Oz perpendiculaire à la piste donne :
-mg cos(θ) + F sin(α) + RN = 0
RN = mg cos(θ) - F sin(α)
D'autre part T = μc RN
donc T = μc (mg cos(θ) - F sin(α))
W() = - mgL sin(θ)
W()= FL cos(α)
W() = 0
W() = - μc L(mg cos(θ) - F sin(α))
D'après le théorème de l'énergie cinétique :
W()+ W(
)+ W(
)+ W(
)=0
- mgL sin(θ) + FL cos(α) - μc L(mg cos(θ) - F sin(α)) = 0
ce qui conduit à :
Bonsoir, merci beaucoup pour cette réponse très détaillée et son shéma ! 
L'expression de la Réaction normale est donc
RN = mg cos(θ) - F sin(α)
avec l'expression de la force trouvée, on a
Rn =
Après mise au meme denominateur, simplification des thermes qui s'annulent au numérateur, ()
et application de la formule de trigo cos a cos b - sin a sin b= cos (a+b) on trouve
Rn =
et T = uc * Rn =
Cela semble t il correct ?
En espérant ne pas avoir inversé des angles θ et α en recopiant la formule
Merci encore
Bonne soirée !
Oui, cela semble correct.
Une vérification rapide est possible à partir des applications numériques.
Avec g = 9,8 N/kg
On trouve F = 266,16N
RN = mg cos(θ) - F sin(α) = 70*9,8*cos(15°) - 266,16*sin(30) = 529,54N
T = µc*RN = 5,295N
Je te laisse le soin de la faire !
Bonsoir,
merci pour votre aide
je trouve effectivement ces valeurs (pour T plutôt 52.95N je pense)
merci encore
très bonne continuation !