Inscription / Connexion Nouveau Sujet
Travail énergie (looping)
Bonjour, j'ai un petit exercice mais je le trouve difficil.
Un point matériel M glisse sans frottements dans une gouttière terminée par une boucle circulaire de rayon R. Calculer la valeur minimale de h pour que la particule abandonnée en A sans vitesse initiale reste en contact avec la goutière tout au long du trajet.
(je suis sencée trouver h> 3R/2)
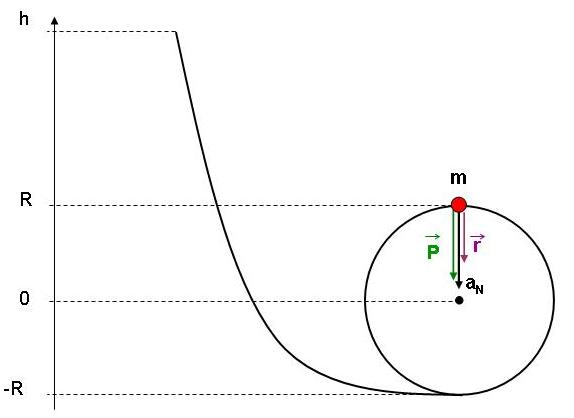
J'ai fait un ptit schéma que le prof nous avait donné pour nous aider:
Merci d'avance
La démarche consiste à déterminer le point le plus problématique dans cette trajectoire (c'est à dire où le risque de décollement est maximal): tu peux peut-être le deviner intuitivement ou sinon, il se calcule...
Ensuite, faire un bilan des forces en ce point afin de déterminer la valeur de la vitesse pour laquelle la valeur de la réaction de la gouttière s'annule et en déduire une condition sur la vitesse minimale nécessaire en ce point.
Enfin, lier la vitesse en ce point à la variation de hauteur par rapport au point de départ grâce à la conservation de l'énergie mécanique et en déduire une condition sur la valeur de h.
A toi de jouer...
J'en déduis que tu n'as pas non plus trouvé intuitivement : il s'agit simplement du sommet du looping où la composante radiale du poids à laquelle est soumise la masse est maximale (égale à ) tandis que sa vitesse est minimale (conformément au principe de conservation de l'énergie mécanique : c'est le point le plus élevé de la trajectoire circulaire et donc celui où l'énergie cinétique est la plus faible).
Si tu regardes la figure que j'ai dessinée, tu peux faire un bilan des forces en ce point et utiliser le principe fondamental de la dynamique pour trouver:
avec : la composante radiale de l'accélération,
: la réaction de la gouttière et
: le poids.
On voit alors que la condition pour que la réaction r reste supérieur à zéro se traduit simplement par:
On sait que sur une trajectoire ciculaire la composante normale de l'accélération est donnée par:
Par ailleurs, entre le point de départ à la hauteur et le sommet du looping on note sur la figure une différence d'altitude égale à h-R.
La vitesse initiale étant nulle, la conservation de l'énergie nous donne donc la vitesse au sommet de la boucle:
la condition pour que la masse ne décolle pas de la gouttière devient donc finalement:
Soit: