Inscription / Connexion Nouveau Sujet
Travail électrostatique
Bonjour,
Trois charges électriques (-q;+q;-q) sont aux trois sommets d'un carré de côté a.
1) Calculer le travail nécessaire pour amener une quatrième charge (+q) depuis l'infini jusqu'au sommet libre.
2) Calculer le travail nécessaire pour assembler cette configuration de quatre charges.
1) J'utilise la formule générale du travail: W= +
+ D F.dl
D F.dl
Ici dl=dr et je ne sais pas quoi mettre pour la force comme à D il n'y a pas de charge.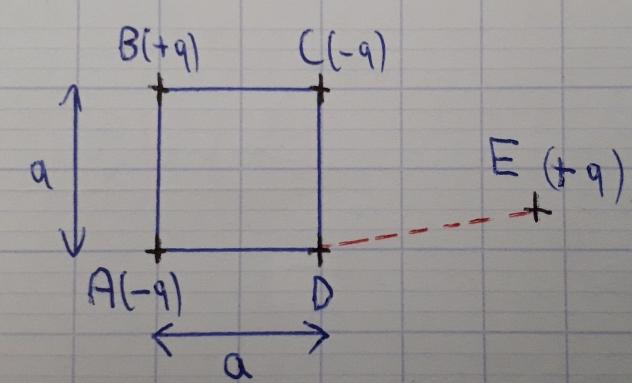
Bonjour
Connais-tu l'expression du travail de la force électrique exercée sur une charge q en fonction de la différence de potentiels ?
Je n'ai pas encore révisé le cours sur les potentiels, je pensais que c'était juste avec les forces, je reviens plus tard.
J'ai une petite question avant de débuter l'exercice: Est-ce que c'est par définition que le champ électrique créé par une charge ponctuelle positive (négative) a une divergence positive (negative), il n'y a pas de démonstration ? (Je vois bien le sens physique qu'une divergence positive signifie que les vecteurs s'éloignent et une divergence négative signifie que les vecteurs convergent)
1) Calculer le travail nécessaire pour amener une quatrième charge (+q) depuis l'infini jusqu'au sommet libre.
1)W=+q[V(D)-V(+ )]=qV(D) avec V(D)-V(+
)]=qV(D) avec V(D)-V(+ )=-
)=- D+
D+ E.dl
E.dl
Ou je dis qV(D)=kq2/r^2  0 ?
0 ?
Je réponds d'abord à propos du travail nécessaire à fournir pour amener une charge q de l'infini en D.
Soit V(M) le potentiel créé en un point M de l'espace par les trois autres charges. Ces trois charges exercent sur la charge q une force électrique Fe dont le travail, lors d'un déplacement d'une position initiale Mi à une position finale Mf s'écrit :
(Attention au signe !)
Pour passer de l'infini où le potentiel créé par les trois autres charges est nul, au point D où le potentiel créé par les trois autres charges est V(D), le travail de la force électrique est donc :
Attention : ce n'est pas ce travail qui est demandé mais celui fourni par un manipulateur extérieur qui provoque le déplacement de l'infini au point D de la charge. Ton énoncé n'est pas très précis mais en général, on suppose que le déplacement s'effectue de façon quasi statique : le mouvement de la charge est suffisamment lent pour que le produit masse par accélération de la charge soit d'influence négligeable. La force exercée par le manipulateur extérieur est donc, en tout point lors du déplacement :
Ces deux forces étant appliquées à la même charge, leurs déplacements sont identiques. On peut donc considérer que les deux travaux sont opposés. Le travail qu'il faut fournir pour amener la charge q de l'infini au point D est donc :
Il te reste, en appliquant le principe de superposition, à déterminer le potentiel en D créé par les trois charges positionnées en A,B et C.
Je te laisse réfléchir à tout cela et proposer une solution.
Concernant la divergence du vecteur champ : attention, en tout point du vide entourant une charge quasi ponctuelle, la divergence du vecteur champ est nulle, ce qui revient à dire que , dans le vide (pas sur la petite boule chargée qui se modélise par une charge quasi ponctuelle), le vecteur champ se comporte comme un vecteur à flux conservatif. C'est pour cette raison que les lignes de champ s'écartent quand on s'éloigne de la charge.
Je ne sais pas trop comment appliquer le théorème de superposition comme c'est un scalaire et pas un vecteur mais je dirais:
V(D)=V(A)+V(B)+V(C)=-2kq/a2 +kq/(a 2)
2)
Donc le travail: W=kq2[-2/a2 +1/a 2]
2]
Il est tout de même plus simple d'additionner des scalaires que des vecteurs ! Je crois que tu as compris.
Attention tout de même à ne pas confondre norme du vecteur champ et potentiel. "a" n'est pas au carré dans le premier terme du potentiel.
D'accord.
2) Calculer le travail nécessaire pour assembler cette configuration de quatre charges.
2) Soit O le centre du carré.
W=WA->O+WB->O+WC->O+WD->O=2WA->O+2WB->O.
WA->O=q[V(A)-V(O)] avec V(A)=2kq/a -kq/a 2
2
V(O)=0
WB->O=-q[V(B)-V(O)] avec V(B)=-V(A)
W=4kq2/a -2kq2/a 2
2
C'est un peu plus subtil...
Placer la charge-q en A ne demande pas de travail car cette charge est la seule dans l'espace.
Placer la charge q en B demande le travail
q.VB où VB est le potentiel en B créé par la seule charge placée en A.
Placer la charge-q en C demande le travail -q.VC où VC est le potentiel en C créé par les deux charges déjà placées.
Tu as déjà exprimé le travail pour placer la charge q en D.
Il te reste à faire la somme de ces travaux.
J'avais mal compris la question, je croyais que je devais assembler ces 4 charges en une seule mais en fait il faut partir du vide et calculer le travail nécessaire à faire cette configuration.
L'ordre dans lequel est-il important ?
Je place A puis B puis C et enfin D.
W=W(A)+W(B)+W(C)+W(D)
W(A)=0
W(B)=q*V(B)=q*-kq/a=-kq2/a
W(C)=-q[V(C)]=-q[kq/a -kq/a 2]
2]
W(D)=kq2[-2/a +1/a 2]
2]
W=-4kq2/a
L'ordre dans lequel est-il important ?
Absolument pas. Cela pourrait d'ailleurs être une méthode de vérification. Tu pourrais vérifier que modifier l'ordre conduit au même résultat.
Le travail ne dépend pas de l'ordre dans lequel on place les charges parce qu'il s'agit du travail d'une force conservative et par définition qui ne dépend pas du chemin suivi mais que de l'état initial et l'état final ?

 ça ma montré un oubli, W=-4kq2/a +2kq2/a
ça ma montré un oubli, W=-4kq2/a +2kq2/a

