Bonjour,

Voilà, j'aurais besoin d'un peu d'aide car je bloque totalement sur mon exercice, alors en espérant tomber sur une personne qui aurait le temps de m'expliquer un peu plus en détail la où je coince.
Merci de votre aide .

Voici l'exercice :

Partie A :

I)

1)  a) Calculer la transformée de Fourier de la fonction f(x)= x.rect(x). On précisera la valeur de f(=0).
    
    b) donner le développement en séries de Fourier de g(x)=x/T rect(x/T)
On donnera les valeurs numériques de c0, c±1, c±2.  Vérification : à quoi correspond c0 et la valeur trouvée vous semble t'elle vraisemblable ? Même question pour c1.

II)

1) Montrer que l'entrée e(t) et la sortie s(t) du filtre représenté ci-dessus sont reliées  par l'équation différentielle :


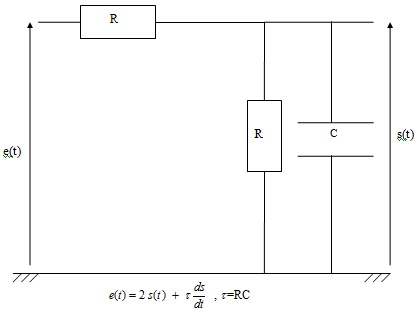
2) Calculer S(p), transformée de Laplace  de s(t)  pour e(t0)=sin(wt) et pour e(t0)=cos(wt), sachant que s(t=0) = 3. Que représente physiquement s(t=0)?

3) Calculer s(t) pour les deux cas de e(t). Vérifiez votre résultat : homogénéité, conditions initiales, valeurs à basse et haute fréquence.


Partie B :

I)

1) Montrer que l'entrée e(t) et la sortie s(t) du filtre représenté ci-dessus sont reliées  par l'équation différentielle :


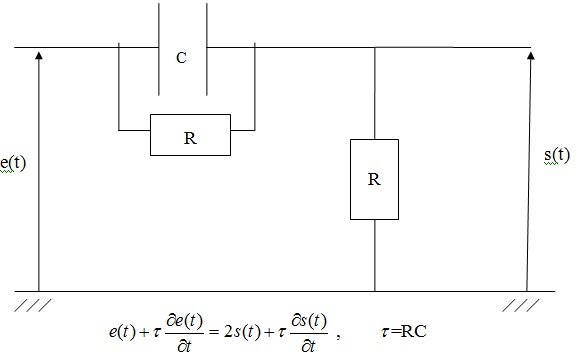
2) Calculer la Transformée de Laplace S(p) de s(t) pour e(t0)=sin(wt), s(t=0)=3

3) Calculer s(t). Vérifiez votre résultat : homogénéité, conditions initiales, valeurs à basse et à haute fréquence.


II)

1) Calculer la transformée de Fourier de la fonction tri(x).

Rappel : tri(x)=1+x, -1<x0 ;   tri(x)=1-x, 0<x<1 ;   tri(x)=0,  

2) Faire le graphe entre x=-2T et x= 2T de la  fonction périodique g(x), de période T, égale  sur l'intervalle  -T/2 < x  T/2 à   :   g(x)=tri(2x/T) , |x| T/2.

3) Donner le développement en séries de Fourier de la  fonction g(x). On donnera, outre une formule générale pour cn,  les valeurs numériques de c0, c1, c-1,c2, c-2.  Que représente c0 et êtes vous satisfait de la valeur trouvée ?