Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... IutForum Supérieur (IUT) PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau iut
Partager :

Transformée de Fourier 2: Corrélation

Posté par
Barth 31-12-12 à 16:56

Bonjour à tous,

Et voilà le nouveau sujet que je voudrai traiter : ** lien vers l'énoncé effacé **


J'ai mit un lien, puisque je ne peux pas reprendre l'image, et je n'ai pas de logiciel d'image sur mon ordinateur.

Donc voilà, la premiére partie est sur la transformée de Fourier, et on est obligé de la faire, puisque la deuxième partie traite de la corrélation par rapport à X(t).

1- Transformée de Fourier:

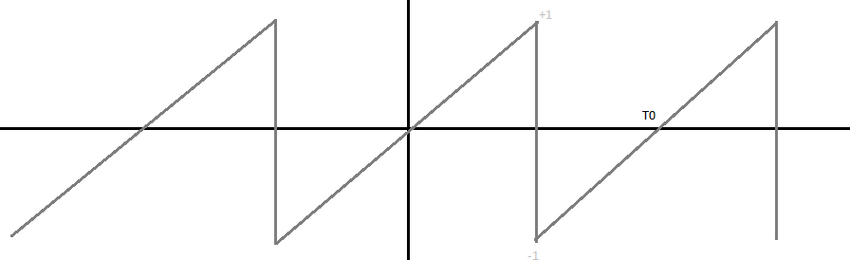
a) Que peut-on dire du signal x(t) ? Et que peut-on en déduire sur sa transformée de Fourier ?
Le signal x(t) semble paire. Donc cela veut dire qu'il n'y a pas de de coefficients b ( impair ) dans la série de coefficients réels/complexes.

b) Calculer les coefficients de la série réelle de Fourier x(t) ?
Il faut calculer a0= (1/T) x(t)dt
Et bien sur an= 2/T x(t).cos(2wt)dt.

Donc pour A0: ( l'intégration se fait de -T0/2 à T0/2.)
Donc il faut d'abord déterminer x(t) qui est une fonction.

Donc x(t)= (y/x)
x(t)= (1/2T0)t. Là on a trouvé a.

Or on doit trouver y = ax + b ?
Donc b = (2To-1)/2T0 ?
Donc x(t) = (1/2T0)t + (2To-1)/2T0 ?

Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum     

Posté par
Barthre : Transformée de Fourier 2: Corrélation 31-12-12 à 16:57

Ou, enfin de compte, je suis en train de me dire que b = 0 non ? Il passe par l'origine en plus ...

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 31-12-12 à 21:06

Bonsoir,
Je n'ai pas le signal x(t) puisque le lien a été supprimé.

Citation :
je n'ai pas de logiciel d'image sur mon ordinateur

Tu as au moins Paint qui existe sous Windows. Ce n'est pas très performant mais faute de mieux...
Tu peux récupérer Gimp sur Internet (gratuit) mais il faut apprendre à l'utiliser...

Posté par
Barthre : Transformée de Fourier 2: Corrélation 01-01-13 à 14:12

Voilà, j'ai fait un schéma de x(t).

Transformée de Fourier 2: Corrélation

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 01-01-13 à 22:53

Citation :
a) Que peut-on dire du signal x(t) ? Et que peut-on en déduire sur sa transformée de Fourier ?
Le signal x(t) semble paire. Donc cela veut dire qu'il n'y a pas de de coefficients b ( impair ) dans la série de coefficients réels/complexes.

Le signal x(t) est périodique. On peut donc le développer en série de Fourier.
Le signal x(t) sur une période est impair. Donc, en intégrant de -T0/2 à T0/2, les coefficients an sont nuls.
Donc a0 = 0 (pas de composante continue) et an = 0   n
\Large b_n\,=\,\int_{-\,\frac{T_0}{2}}^{\frac{T_0}{2}}x(t)\,sin(n\omega_0t)\,dt

\Large x(t)\,=\,\frac{2}{T_0}\,t    pour  \Large -\,\frac{T_0}{2}\,\le\,t\,\le\,\frac{T_0}{2}

\Large \omega_0\,=\,\frac{2\,\pi}{T_0}

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 02-01-13 à 03:03

Plus exactement :
\Large b_n\,=\,\frac{2}{T_0}\,\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}x(t)\,sin(n\omega_0t)\,dt

Posté par
Barthre : Transformée de Fourier 2: Corrélation 02-01-13 à 10:17

Ah, le signal est impair puisqu'il passe par 0 ?

Sinon, pour x(t), j'ai vu mon erreur, et je trouve la même chose x(t) = 2/T0 t

b) bn= (2/T0)x(t)sin(nw0t) dt ( entre -T0/2 et T0/2 ).
Il faut fa

Posté par
Barthre : Transformée de Fourier 2: Corrélation 02-01-13 à 10:37

Il faut faire une intégration par partie.

avec u= sin(nw0t) ; u'= -(1/nw0)cos(nw0t)
v = 2/T0 t et v'= 2/T0.

Et je trouve le résultat suivant: 4/nT0.

c) Il faut rappeler l'expression des coefficients de la série complexe de Fourier en fonction de ceux de la série réelle de Fourier et en déduire l'expression de x(t):

Cn = (An - iBn)/2

Or pas de An car impair, donc il reste Cn = -iBn/2

Donc Cn = 2/nT0.

d) Préciser le motif m(t) du signal x(t) ? Et exprimer x(t) à partir de m(t) et d'un peigne de Dirac ?

Un peigne de Dirac : ( (t-nT) ?
Un motif: Carrée, triangle ?

Donc je pense que m(t)est un carré d'amplitude 2/n.
Et le peigne de Dirac:
n = (t)exp(-j2n(1/T0)) et qui est égale à 1/T0.

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 02-01-13 à 14:33

Citation :
Ah, le signal est impair puisqu'il passe par 0 ?

Une fonction paire ou impaire n'a pas de rapport direct avec le fait qu'elle passe par 0 ou non...
La définition d'une fonction paire est   : f(-x) = f(x) (parabole par exemple).
La définition d'une fonction impaire est : f(-x) = -f(x) ( f(x) = ax ou f(x) = a x3 par exemple) .
Le produit de deux fonctions paires ou de deux fonctions impaires est pair.
Le produit d'une fonction paire et d'une fonction impaire est impair.
Pour les bn, je trouve :
\Large b_n\,=\,(-1)^n\,\frac{2}{n\,\pi}
Donc les Cn :
\Large c_n\,=\,-\,i\,\frac{b_n}{2}\,=\,i\,(-1)^n\,\frac{1}{n\,\pi}

Pour la d :
Le motif, c'est le motif qui se répète autrement dit la période. Le motif est une rampe.
\Large m(t)\,=\,\frac{2}{T_0}\,t    pour  \Large -\,\frac{T_0}{2}\,\le\,t\,\le\,\frac{T_0}{2}
Avec le peigne de Dirac :
\Large x(t)\,=\,m(t)\,*\,\sum_{n=-\infty}^{+\infty}\delta(t-nT_0)
*  étant la convolution

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 02-01-13 à 14:34

\Large *  indique la convolution et non pas la multiplication.

Posté par
Barthre : Transformée de Fourier 2: Corrélation 02-01-13 à 20:22

J'ai du mal à comprendre comment tu arrives à ce résultat pour bn ?

Puisque 2/T0 ( [(2/T0)tsin(nw0t)] - (2/T0)sin(nw0t) ) entre -T0/2 et T0/2.

Le terme de droite s'annule. Il reste celui de droite. Et à l'avant de l'intégrale, j'ai du (2/T0)².

Tu as dérivé le (2/T0)t et tu as fait la primitive de sin(nw0t) pour les u et v ?

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 02-01-13 à 21:34

Oui, c'est ça...
\Large b_n\,=\,\frac{2}{T_0}\,\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}x(t)\,sin(n\omega_0t)\,dt
\Large b_n\,=\,\frac{2}{T_0}\,\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}\frac{2}{T_0}\,t\,sin(n\omega_0t)\,dt
\Large b_n\,=\,\left(\frac{2}{T_0}\right)^2\,\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}t\,sin(n\omega_0t)\,dt


\Large \int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}t\,sin(n\omega_0t)\,dt\,=\,\left[-t\frac{1}{n\omega_0}cos(n\omega_0t)\right]_{-\frac{T_0}{2}}^{\frac{T_0}{2}}\,+\,\frac{1}{n\omega_0}\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}cos(n\omega_0t)\,dt\,=\,\left(-\frac{T_0}{2n\omega_0}cos(n\pi)\,-\,\frac{T_0}{2n\omega_0}cos(-n\pi)\right)\,+\,\frac{1}{(n\omega_0)^2}\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}n\omega_0\,cos(n\omega_0t)\,dt
u=t\,\Rightarrow\,du=dt
dv=sin(n\omega_0t)\,dt\,\Rightarrow\,v=-\frac{1}{n\omega_0}cos(n\omega_0t)
\Large \int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}t\,sin(n\omega_0t)\,dt\,=\,-\,\frac{T_0}{n\omega_0}cos(n\pi)\,+\,\frac{1}{(n\omega_0)^2}\,\left[sin(n\omega_0t)\right]_{-\frac{T_0}{2}}^{\frac{T_0}{2}}
\Large \int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}t\,sin(n\omega_0t)\,dt\,=\,-\,\frac{T_0}{n\omega_0}(-1)^n\,+\,\frac{1}{(n\omega_0)^2}\,\left(sin\left(n\frac{2\pi}{T_0}\frac{T_0}{2}\right)\,-\,sin\left(-n\frac{2\pi}{T_0}\frac{T_0}{2}\right)\right)
\Large \int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}t\,sin(n\omega_0t)\,dt\,=\,-\,\frac{T_0}{n\omega_0}(-1)^n\,+\,\frac{1}{(n\omega_0)^2}\,\left(sin\left(n\pi\right)\,-\,sin\left(-n\pi\right)\right)
\Large \int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}t\,sin(n\omega_0t)\,dt\,=\,-\,\frac{T_0^2}{2n\pi}(-1)^n
Donc :
\Large b_n\,=\,\frac{4}{T_0^2}\,\left(-\,\frac{T_0^2}{2n\pi}(-1)^n\right)

\Large \boxed{b_n\,=\,-\,(-1)^n\,\frac{2}{n\pi}}

Ouf ! je suis arrivé au bout et sans erreur, je crois...

Posté par
Barthre : Transformée de Fourier 2: Corrélation 03-01-13 à 10:13

Ok ! J'ai vu où je me suis planté ( enfin erreur de signe, étourderie ... )

Alors pour la d)

x(t) = m(t) * (t-nT0)
x(t) est tout simplement égale à la somme de m(t)*(t-nT0)
Donc x(t) = Somme ( 2/T0(t-nT0) ?

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 03-01-13 à 18:34

Pas toujours facile le calcul sur les séries de Fourier... C'est souvent très calculatoire.
Il en est de même des transformées de Fourier...

Pour la d, oui mais il faut l'écrire comme je l'ai écrit pour répondre à la question.

\Large\boxed{ x(t)\,=\,m(t)\,*\,\sum_{n=-\infty}^{+\infty}\delta(t-nT_0)}
avec
\Large m(t)\,=\,\frac{2}{T_0}\,t    pour  \Large -\,\frac{T_0}{2}\,\le\,t\,\le\,\frac{T_0}{2}
Une convolution par \delta(t-nT_0) décale le signale de  nT_0.
Si n = 1, on a une convolution par \delta(t-T_0) donc le signal est décalé (vers la droite) de T0.
Si n = 2, on a une convolution par \delta(t-2T_0) donc le signal est décalé (vers la droite) de 2 T0.
Si n = -1, on a une convolution par \delta(t+T_0) donc le signal est décalé (vers la gauche) de T0.
etc...

Posté par
Barthre : Transformée de Fourier 2: Corrélation 03-01-13 à 20:02

D accord, donc c'est juste ça.

Après il faut alors calculer la TF M(f) du motif m(t) puis en déduire les coefficients de la série complexe de Fourier X(f), transformée de x(t).

Donc pour m(t) il faut l'intégré de -T0/2 à T0/2 ? Ou il faut ( en plus ) le multiplier par un sinus ?
X(f) on l'a calculé un peu plus haut dans les posts.

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 03-01-13 à 22:19

\Large TF\left(x(t)\right)\,=\,TF\left(m(t)\,*\,\sum_{n=-\infty}^{+\infty}\delta(t-nT_0)\right)
\Large TF\left(x(t)\right)\,=\,TF\left(m(t)\right)\,.\,TF\left(\sum_{n=-\infty}^{+\infty}\delta(t-nT_0)\right)
\Large \boxed{X\left(f\right)\,=\,TF\left(x(t)\right)\,=\,TF\left(m(t)\right)\,.\,\frac{1}{T_0}\,\sum_{k=-\infty}^{+\infty}\delta(f-\frac{k}{T_0})}

Avec :
\Large TF\left(m(t)\right)\,=\,\int_{t=-\frac{T_0}{2}}^{\frac{T_0}{2}}m(t)\,e^{-\,j2\pi f t}dt
\Large \boxed{M\left(f\right)\,=\,TF\left(m(t)\right)\,=\,\frac{2}{T_0}\int_{t=-\frac{T_0}{2}}^{\frac{T_0}{2}}t\,e^{-\,j2\pi f t}dt}

Posté par
Barthre : Transformée de Fourier 2: Corrélation 04-01-13 à 09:48

Donc pour la TF de m(t):

je suis arrivé à 2 (( -exp(-jfT0) - exp(jfT0) )/ jf) - ( exep(-jfT0) + exp(jfT0) )/ 2²f²T0.

La bonne nouvelle, c'est comme on doit trouver des résultats sous la forme complexe, sa va. Mais sinon, si je me suis pas trompé, je ne sais pas quoi en faire de ça.

Posté par
Barthre : Transformée de Fourier 2: Corrélation 04-01-13 à 16:16

2) Corrélation

a) Donner l'expression du calcul direct de la fonction d'autocorrélation de x(t) c'est bien cette formule ?

( - à + ) x(t)*x(t+) ?

Posté par
Barthre : Transformée de Fourier 2: Corrélation 05-01-13 à 16:45

Personne ?

Je pose les autres questions si quelqu'un veut répondre, puisque je suis complétement bloqué !

b) Exprimer la fonction d'autocorrélation à partir de x(t) et de l'opération de convolution. Montrer que phix(t) = -m(t)*m(t)*delta2T0(t) ?

Calculer phim(t) = -m(t)*m(t)? Que représente phim(t) ?

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 05-01-13 à 22:19

Je vais répondre mais j'ai bloqué par d'autres tâches incontournables... Désolé...

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 05-01-13 à 22:19

"j'ai bloqué" ==> j'ai été bloqué

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 05-01-13 à 22:35

On trouve :
\Large M(f)\,=\,TF(m(t))\,=\,-\,\frac{T_0}{4j\pi f}\left(e^{-j\pi fT_0}\,+\,e^{j\pi fT_0} \right)\,+\,\frac{1}{4\pi^2f^2}\left(e^{-j\pi fT_0}\,-\,e^{j\pi fT_0} \right)
Ensuite, il faut utiliser les formules d'Euler pour transformer ça en cosinus et en sinus.

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 05-01-13 à 22:45

Il en manque un bout...

\Large \boxed{M\left(f\right)\,=\,TF\left(m(t)\right)\,=\,\frac{2}{T_0}\int_{t=-\frac{T_0}{2}}^{\frac{T_0}{2}}t\,e^{-\,j2\pi f t}dt}

\Large M\left(f\right)\,=\,\frac{2}{T_0}\int_{t=-\frac{T_0}{2}}^{\frac{T_0}{2}}t\,e^{-\,j2\pi f t}dt}\,=\,\frac{2}{T_0}\left(-\,\frac{T_0}{4j\pi f}\left(e^{-j\pi fT_0}\,+\,e^{j\pi fT_0} \right)\,+\,\frac{1}{4\pi^2f^2}\left(e^{-j\pi fT_0}\,-\,e^{j\pi fT_0} \right)\right)

Posté par
Barthre : Transformée de Fourier 2: Corrélation 06-01-13 à 10:19

Ne t'inquiètes pas, c'est pas grave, même si je suis un peu plus " pressé " puisque j'ai partiel demain. Et l'auto-corrélation, j'ai beaucoup de mal.
Oui d'accord, donc on a en faite:

X(f) = - cos ( jfT0 - sin(jfT0) ?

2) Corrélation

a) Donner l'expression du calcul direct de la fonction d'autocorrélation de x(t) c'est bien cette formule ?

( - à + ) x(t)*x(t+) ?


b) Exprimer la fonction d'autocorrélation à partir de x(t) et de l'opération de convolution. Montrer que phix(t) = -m(t)*m(t)*delta2T0(t) ?

Calculer phim(t) = -m(t)*m(t)? Que représente phim(t) ?

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 06-01-13 à 12:45

Je te réponds vers 16h...
Pour X(f), c'est un peu plus compliqué que ça... Les coeffs des cosinus et sinus ne sont pas bons.
Pour l'autocorrélation, il faudrait préciser la variable d'intégration (bon d'accord, c'est t mais encore faut-il l'écrire...)

Posté par
Barthre : Transformée de Fourier 2: Corrélation 06-01-13 à 13:24

Merci d'avance !

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 06-01-13 à 19:06

Un peu de retard...
\Large M(f)\,=\,\frac{2}{T_0}\,\left(-\frac{T_0}{2j\pi f}\,cos(\pi f T_0)\,+\,\frac{1}{j2\pi^2f^2}\,sin(\pi f T_0) \right)
Donc :
\Large X(f)\,=\,M(f)\,.\,\frac{1}{T_0}\sum_{k=-\infty}^{+\infty}\delta\left(t-\frac{k}{T_0} \right)
\Large X(f)\,=\,\frac{2}{T_0^2}\,\left(-\frac{T_0}{2j\pi f}\,cos(\pi f T_0)\,+\,\frac{1}{j2\pi^2f^2}\,sin(\pi f T_0)\right).\sum_{k=-\infty}^{+\infty}\delta\left(t-\frac{k}{T_0} \right)
Pour  \Large f\,=\,\frac{k}{T_0} :
\Large \Rightarrow\,C_k\,=\,-\,\frac{1}{jk\pi}(-1)^k
Pour  \Large f\,=\,-\,\frac{k}{T_0} :
\Large \Rightarrow\,C_{-k}\,=\,\frac{1}{jk\pi}(-1)^k
et :
\Large b_n\,=\,j\left(C_n\,-\,C_{-n}\right)
On retrouve les   b_n  calculés par la série de Fourier (quand on fait le calcul).
Je te mets le calcul si tu en as besoin mais j'en ai pour un moment à l'écrire.

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 06-01-13 à 19:17

L'autocorrélation de x(t) :
- formule directe :
\Large R_x(\tau)\,=\,\int_{-\infty}^{+\infty}x(t+\tau)\,x^*(t)\,dt\,\,\,\,\textrm{ou}\,\,\,\,R_x(\tau)\,=\,\int_{-\infty}^{+\infty}x(t)\,x^*(t-\tau)\,dt
- avec la convolution :
\Large x(t)\,*\,x(-t)
* étant la convolution  (et non pas le produit)

Citation :
Montrer que phix(t) = -m(t)*m(t)*delta2T0(t) ?

" delta2T0(t) " ==> je ne comprends pas ça...
Ne serait-ce pas  2\,T_0\,\delta(t)  ?

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 06-01-13 à 19:25

Citation :
- avec la convolution :
\Large x(t)\,*\,x(-t)

J'ai oublié quelque chose !...
- avec la convolution :
\Large x(t)\,*\,x^*(-t)
* étant la convolution  (et non pas le produit) et  x^*  étant le conjugué de x(t)

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 06-01-13 à 19:42

Citation :
Calculer phim(t) = -m(t)*m(t)? Que représente phim(t) ?

m(t) étant un réel, on a   m^*(t)\,=\,m(t)     ( m^*(t)  étant le conjugué de  m(t) )
m(t) étant impaire, m(-t) = - m(t).
Donc m^*(-t)\,=\,- m(t)
Donc :
\large \phi_{m(t)}\,=\,-\,m(t)\,m(t)\,=\,m(t)\,(-\,m(t))\,=\,m(t)\,*\,m^*(-t)
\large \phi_{m(t)}    est la fonction d'autocorrélation de m(t)

Posté par
Barthre : Transformée de Fourier 2: Corrélation 06-01-13 à 20:36

Oui c'est bien 2T0 (t) 2T0 est en indice ... Et je ne comprend pas non plus.

Posté par
Barthre : Transformée de Fourier 2: Corrélation 06-01-13 à 20:40

Tu trouverais quoi en faisant le calcul de l'auto-corrélation ? c'est possible qu'il y est une erreur dans le sujet !

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 06-01-13 à 21:26

Citation :
Donc :
\large \phi_{m(t)}\,=\,-\,m(t)\,m(t)\,=\,m(t)\,(-\,m(t))\,=\,m(t)\,*\,m^*(-t)

Je rectifie... J'ai confondu convolution et multiplication...
\large \phi_{m(t)}\,=\,-\,m(t)\,m(t)\,=\,m(t)\,(-\,m(t))\,=\,m(t)\,\,m^*(-t)
\Large \int_{-\infty}^{+\infty}m(t+\tau)\,m^*(t)\,dt\,=\,\int_{-\infty}^{+\infty}-\,m(t+\tau)\,m(t)\,dt

\large \phi_{m(t)}  est la fonction d'autocorrélation de m(t) en t = 0

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 06-01-13 à 21:31

en \tau\,=\,0 , pardon...
Enfin tu peux l'écrire aussi :
\Large \int_{-\infty}^{+\infty}m(\tau+t)\,m^*(\tau)\,d\tau\,=\,\int_{-\infty}^{+\infty}-\,m(\tau+t)\,m(\tau)\,d\tau

\large \phi_{m(t)}  est la fonction d'autocorrélation de m(t) en t = 0

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 06-01-13 à 21:38

Citation :
Montrer que x(t) = -m(t) m(t) 2T0(t) ?

Quelle est la définition de x(t) ?
Pour le calculer, on est bien obligé de savoir ce que c'est !

Posté par
Barthre : Transformée de Fourier 2: Corrélation 07-01-13 à 18:45

Et bien j'ai passé le partiel de traitement du signal 2. Je pense que cela s'est bien passé. Donc je te remercie de ton aide !

Posté par
Aragornre : Transformée de Fourier 2: Corrélation 07-01-13 à 18:48

Eh bien, tant mieux !...


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !