Inscription / Connexion Nouveau Sujet
transformation intégrale
Bonjour à vous.
Je dois trouver la fonction de transfert de ce circuit en passant par la transformée de Laplace en utilisant l'équation différentielle de ce circuit
mon premier souci est sur les mailles:
De la première entre R1, L1, et C1 où j'exprime ve(t)=f (vC1 (t)):
Ve (t)= R1C1dvC1/dt+l1c1d2vc1/[dt]+vc1
De la seconde maille C1, L2, C2 où j'exprime vc1=f (vc2), jobtiens:
Vc1= vc2 + l2c2dvc2/dt
de la dernière maille R1, L1, R1, C2, R2, où j'exprime ve(t)=f (vs(t))
Ve (t)=(R1/R2) Vs + L1 (R1/R2) dvs/dt + vc2 + vs
maintenant je sais pas comment combiner les relations (je sais pas déjà si c'est juste ce que j'ai fait) pour obtenir une équations finale ve=f (vs) et où j'aurais tous les paramètres R1, R2, L1, L2, C1, C2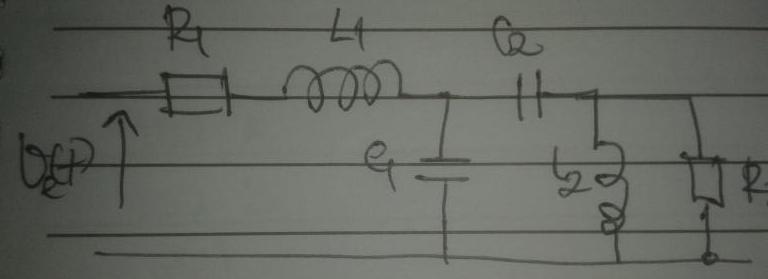
***Image recadrée***
Bonsoir
Il y a bien une méthode très simple consistant à travailler d'abord en régime sinusoïdal. Tu exprimes l'impédance complexe Z1 de l'association[R1,L1) puis l'impédance complexe Z2 de l'association {C1 // L2 //R2}. La fonction de transfert complexe est (formule du diviseur de tension) :
Il te suffit ensuite de remplacer j
par "p".
Cette méthode est en général acceptée...
Aïe ! j'ai posté trop vite ! Je n'ai pas tenu compte de C2 ! Mais la méthode consistant par raisonner d'abord en régime sinusoïdale reste valide.
Il faut d'abord obtenir l'expression de la tension U entre la masse et le nœud commun à L1,C1,C2. C'est à cette tension U qu'il faut appliquer la formule du diviseur de tension :
où ZB désigne l'impédance de l'association (L2 //R2).
Cela va être assez calculatoire mais à mon avis nettement moins que d'appliquer les lois des nœuds et des mailles en raisonnant sur les valeurs instantanées...
Merci mais le problème est que on est en régime transitoire donc je peux pas utiliser les impedances complexes
Tu dois savoir qu'en régime sinusoïdal, multiplier par (j)n la valeur complexe associée à une tension est équivalent à prendre la dérivée nième de cette tension par rapport au temps. Raisonner en régime sinusoïdal permet donc d'obtenir l'équation différentielle valide en régime sinusoïdal. On admet alors que cette équation différentielle, démontrée en régime sinusoïdal, est valide en régime variable quelconque.
Exemple : imagine que le circuit étudié en régime sinusoïdal conduise à :
A.(j)3.Vs+B.(j)2.Vs+C.Vs=D.(j).Ve
avec A,B,C,D des valeurs dépendant des caractéristiques des différents dipôles; l'équation différentielle vérifiée par vs(t) est :
Soit, en notations de Laplace :
Cet exemple est choisi totalement au hasard. La situation que tu dois étudier est beaucoup plus compliquée. Je me demande si celui qui a posé cet exercice en a bien mesuré tout l'aspect "calculatoire"...
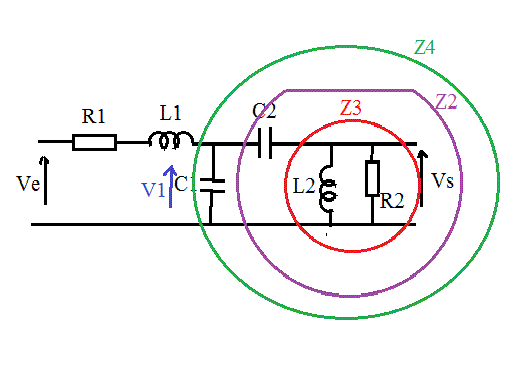
Z3 = p.R2.L2/(R2 + pL2)
Z2 = 1/(p.C2) + Z3
Z2 = 1/(p.C2) + p.R2.L2/(R2 + pL2)
Z2 = (R2 + pL2 + p².R2.L2.C2)/(pC2.(R2+pL2))
Z4 = ((Z2)/(pC1))/(Z2 + 1/(pC1))
Z4 = z2/(1 + pC1.Z2)
Z4 = (R2 + pL2 + p².R2.L2.C2)/[p(R2C2+R2C1) + p²(L2C2+L2C1) + p³(R2L2C1C2)]
V1/Z4 = Ve/(R1+pL1 + Z4)
V1 = Ve * Z4/(R1+pL1+Z4)
V1/Z4 = Vs/Z3
Ve/(R1+pL1+Z4) = Vs/Z3
Vs/Ve = Z3/(R1+pL1+Z4)
Et on a déterminé Z3 et Z4, donc ...
On a donc Vs/Ve en fonction de p.
On peut ensuite remplacer p par d/dt, p² par d²/dt², p³ par d³/dt³ ...
pour avoir une équation différentielle en fonction du temps.
Aucun calcul vérifié ... et donc à faire.
Mais le principe est bon.
Annuler
connectez vous