Inscription / Connexion Nouveau Sujet
Transformateur Monophasé
Bonjour,
voila je suis bloqué à la troisième partie d'un exercice dont voici l'énoncé:
Un transformateur monophasé 110V/220V; 50Hz, a donné aux essais les résultats suivants:
-essai à vide: U10=110V; 50Hz; I10=3,0A; U20=220V et P10=67 Watts
-essai en court-circuit:U1cc=7 V; I1cc=20A et P1cc= 105W
3.Le primaire est soumis à la tension nominale de valeur efficace U1=110V. Calculer la valeur efficace U2 de la tension secondaire:
intensité efficace du courant secondaire I2=10A et facteur de puissance secondaire cos =1
=1
Voila, j'espère que vous pourrez m'aider, merci d'avance.
PS: Venant d'un section générale je n'ai pas les bases de l'électrotechnique.Par conséquent j'ai quelques lacunes d'ou mes diffiucltés sur cet exercice.
Bonjour,
Pourriez vous présenter le texte complet de votre exercice ainsi que vos premiers résultats ?
A vous lire. JED.
Bien sûr, voici tout d'abord l'énoncé complet:
Un transformateur monophasé 110V/220V; 50Hz, a donné aux essais les résultats suivants:
-essai à vide: U10=110V; 50Hz; I10=3,0A; U20=220V et P10=67 Watts
-essai en court-circuit:U1cc=7 V; I1cc=20A et P1cc= 105W
1.Calculer:
1.1 le rapport de transformation;
1.2 Le facteur de puissance à vide.
2.Dans l'hypothèse ou l'on néglige l'intensité efficace du courant à vide par rapport à l'intensité efficace du courant primaire lorsque le transformateur fonctionne en charge (hypothèse de Kapp):
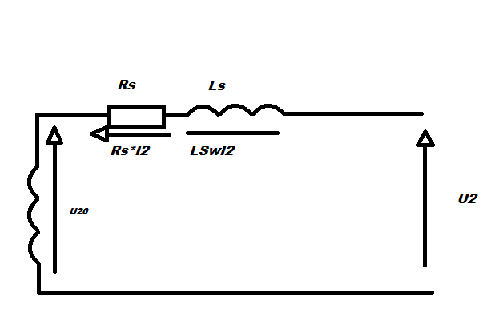
2.1donner un schème équivalent du transfomateur (modèle de Thévenin) vu des bornes du secondaire, en précisant la signification des éléments y figurant;
2.2donner la relation entre les vecteurs de Fresnel associés à la tension secondaire, et aux différentes tension aux bornes des éléments du schéma équivalents.
2.3Calculer les valeurs numériques des éléments du schéma équivalent.
3.Le primaire est soumis à la tension nominale de valeur efficace U1=110V. Calculer la valeur efficace U2 de la tension secondaire:
3.1.intensité efficace du courant secondaire I2=10A et facteur de puissance secondaire cos=1
3.2.intensité efficace du courant secondaire I2=5.0A et facteur de puissance secondaire cos=0.80, la charge étant inductive
4.Calculer le rendement du transformateur lorsqu'il fonctionne dans les conditions définies à la question 3.2.
5.Le secondaire du transformateur alimente une charge inductive réglable dont le facteur de puissance cos 2 est maintenu constant et égal à 0.80.Le primaire est toujours soumis à sa tension nominale de valeur efficace U1=110V. Calculer:
2 est maintenu constant et égal à 0.80.Le primaire est toujours soumis à sa tension nominale de valeur efficace U1=110V. Calculer:
5.1L'intensité efficace I2 du courant secondaire pour laquelle le rendement du transformateur est maximal;
5.2ce rendement, sachant que la valeur efficace de la tension secondaire est alors U2'=209V.
Maintenant voici mes premiers résultats:
1.1 m=U2/U1=220/110=2
1.2 Fp=P/S=P10/(U10*I10)=0.2
2.1Voir dessins ci dessous
2.2 U20=Rs*I2+LS I2+U2
I2+U2
2.3 Rs=P1cc/I2cc2=105/102=1.05
or I2cc=I1cc/m d'ou I2cc=20/2=10
Ls=( U2cc2-(Rs*I2cc2))/(
U2cc2-(Rs*I2cc2))/( *I2cc)
*I2cc)
=( 142-(10,52))/(3141.5)
142-(10,52))/(3141.5)
=( 196-110.25)/(3141.5)
196-110.25)/(3141.5)
=( 87.75)/3141.5
87.75)/3141.5
=0.0029H=2.9mH
m=U2cc/U1cc d'ou U2cc=m*U1cc
=2*7=14V
Voila pour les résultats j'espère que vous pourrez m'aider merci d'avance
Bonsoir,
Tout d'abord merci d'avoir fait parvenir le texte de votre exercice.
Les réponses des questions 1 et 2 sont toutes correctes.
Pour la 3 il faut utiliser le diagramme de Kapp.
Il est basé sur la relation vectorielle : -mU1 = RsI2 + LwI2 +U2 A voir dans votre cours.
31 RsI2 = 10,5 V LwI2 = 9,3 V mU1 = 220 V cosphi2 =1 donc U2 sera un vecteur "horizontal".
Construction :
10,5 horizontal
9,3 vertical
A partir de l'origine de 10,5 vous faites un cercle de rayon 220?
A partir de l'extrémité de 9,3 vous faites une horizontale qui coupe le cercle et vous obtenez U2. (phi2 = 0).
Pour 32 vous faites la construction en tenant compte de cosphi2 = 0,8.
Pour la suite des indications seront données demain matin. Bon courage. JED.
Merci Beaucoup, j'ai très bien compris ce que vous avez avez écrit toutefois:
"A partir de l'origine de 10,5 vous faites un cercle de rayon 220?"
ça n'est pas possible à moins de réduire l'échelle c'est pourquoi je propose d'utiliser la formule suivante:
 U=Rs*I2*cos
U=Rs*I2*cos +Ls
+Ls I2*sin
I2*sin
On obtient alors  U de manière approximative et ensuite:
U de manière approximative et ensuite:
U20-U2= U2
U2
Ainsi on trouve U2 non?
Pour la suite je veux bien des indications pour toutes les questions restantes car elles ne sont pas évidente.
Merci beaucoup de m'avoir répondu JED
Alors par le calcul voila mes réponses:
3.1 U2=10.5*1+9.1*0 car cos
U2=10.5*1+9.1*0 car cos =1
=1
d'ou  =cos-1(1)=0
=cos-1(1)=0
 U2=10.5
U2=10.5
U20-U2= U2
U2
220-U2=10.5
-U2=10.5-220
-U2=-209.5
U2=209.5 V
3.2 U2=5.25*0.8+4.5*0.58 car cos
U2=5.25*0.8+4.5*0.58 car cos =0.8
=0.8
d'ou  =cos-1(0.8)=36
=cos-1(0.8)=36
 U2=4.2+13.22=17.42
U2=4.2+13.22=17.42
U20-U2= U2
U2
220-U2=17.42
-U2=17.42-220
-U2=-202.5
U2=202.5 V
voila les résultats me paraissent bizarre donc j'ai voulu essayer avec votre méthode mais même en réduisant l'échelle par 10 je n'y parviens pas.
Bonjour,
Vous avez raison , la construction du diagramme de Kapp n'est pas toujours facile à réaliser. En effet RsI2 et LwI2 sont très
faibles devant les autres tensions.
Pour ma part j'ai réalisé les constructions avec 1 cm pour 20 V. Pour cosphi2 =1 j'ai trouvé U2 = 208 V et 206 V pour cosphi2=0,8.
Ce sont des valeurs à vérifier.
4-
Pour le rendement.
P2 =U2I2cosphi2................
pertes fer, indépendantes de la charge, essai à vide............F =......
Pertes cuivre (joule), essai en court-circuit, C.
ATTENTION, C = k*I2^2
20 A.......>105 W 5 A.........> C =....
D'où le rendement.
5-
51 Le rendement est maximal quand C = F donc C = 67 W
Avec l'idée du 4 vous trouverez le nouvel I2.
52 Vous recalculez P2 puis le rendement.
Bon courage. JED.
Bonjour,
pour les questions 3.1 et 3.2 j'ai trouvé a peu prés les mêmes valeurs.
Voici ce que j'ai pour la question 4:
P2=U2I2Cos 2
2
P2=206*5*0.80=820
Pur l'essai à vide les pertes fers représente P10 soit 67W car elles sont indépendantes de la charge essai à vide.
Les pertes joules sont égales à RsI22=52*1.05=26.25.
On a donc le  =P2/(P2+Pf+PJ)
=P2/(P2+Pf+PJ)
 =0.89
=0.89
Le résultat me parait cohérent dans la mesure ou le rendement est inférieure ou égale à 1 dans le meilleur des cas.
Pour la question 5.1:
Je sais que P2=U2I2'cos 2
2
PJ=RsI2' et Pf=67
Nous on veut I2' donc on utilise la formule du rendement:
 =P2/(P2+Pf+Pc)
=P2/(P2+Pf+Pc)
On introduit I2' dans la formule:
 =(P2/I2')/((P2/I2')+(Pf/I2')+(Pc/I2'))
=(P2/I2')/((P2/I2')+(Pf/I2')+(Pc/I2'))
 =(P2cos
=(P2cos 2)/((P2cos
2)/((P2cos 2)+(Pf/I2')+(RsI2')
2)+(Pf/I2')+(RsI2')
si le  est maximum ça veut dire qu'il est égale à 1?
est maximum ça veut dire qu'il est égale à 1?
on aurait donc: 1=1/(Pf/I2')+(RsI2')
c'est à dire 1=(Pf/I2')+(RsI2')
soit (Pf/I2')=(RsI2')?
d'où 2I2'=Pf/Rs
2I2'=67/1.05=63.8 donc I2'=31.9=32 A
Voila je ne suis du tout sur de moi pour cette question
Pour finir la question 5.2
P2=U2'I2'cos 2=5350.4
2=5350.4
Pf=67
et Pj=1.05*322=1075.2 j
 =5350.4/(5350.4+67+1075.2)=0.82
=5350.4/(5350.4+67+1075.2)=0.82
Voila reste à savoir si tout cela est correct 
Bonsoir,
4/ P2 d'accord Pf d'accord
Pj NON ces pertes sont de la forme Pj = kI2^2
20 A.......>105 W 5A......>Pj =(105*25)/400 = 6,6 W
D'où un rendement de 0,92
5/ Pas d'accord. Vous trouvez 0;89 puis 0,82 donc il y a un problème.
Le rendement est maximal pour Pf = Pc = 67 W
Pc= kI2^2
20 A......> 105 W donc 105= 400k et 67 = I2^2*K I2 = 16 A
Continuez P2 puis le rendement. Bon courage. JED.
PS: ne partez surtout pas de l'idée que le rendement maximal est égal à 1. Quoique beaucoup de machines électriques ont un
excellent rendement voisin de 1.



