Inscription / Connexion Nouveau Sujet
trajectoire satellite
Bonjour
Je dois résoudre un exercice voici l'énoncé : un satellite artificiel decrit autour de la terre une orbite circulaire de rayon h. En un point A un pilote declenche une poussée retrograde pendant un temps tres court de telle facon qu'il puisse aterrir en un point B de la terre, tel que l'angle entre OA et OB soit droit. O le centre de la terre. Determiner la trajectoire entre les points A et B. Expliciter les vitesses du satellite avant et apres freinage en fonction de h, de R rayon de la terre et g pesanteur au niveau du sol.
J'ai essayé de faire une etude sur le systeme S, un bilan des forces puis un pfd, mais rien a faire. On connait pas l'expression de la force de freinage. De plus jai un autre souci, je ne sais pas comment mais je sais qu'on le doit mais je ne vois absolument pas comment exploiter cette hypothese d'angle droit !!
Une petite aide de votre part me sera grandement utile!
bonsoir,
après le freinage la trajectoire ne peut plus être circulaire, donc quelles sont les autres possibilités de trajectoire? (si on se place dans le cadre d'un mvt képlérien):
et quelle est la seule possible dans ce cas précis?
Bsr
Merci d'avoir répondu ! Bah je doute que la trajectoire ne soit plus circulaire mais elliptique mais dans ce cas comment le demontrer ?? Je me dis que il faut utiliser l'hypothèse de l'angle droit mais comment ? Je bloque complement, le pfd ni le tem ne marchent....
la trajectoire est forcément une ellipse puisque la vitesse après le freinage est inférieure à celle correspondant à la trajectoire circulaire, et donc inférieure à la vitesse de libération
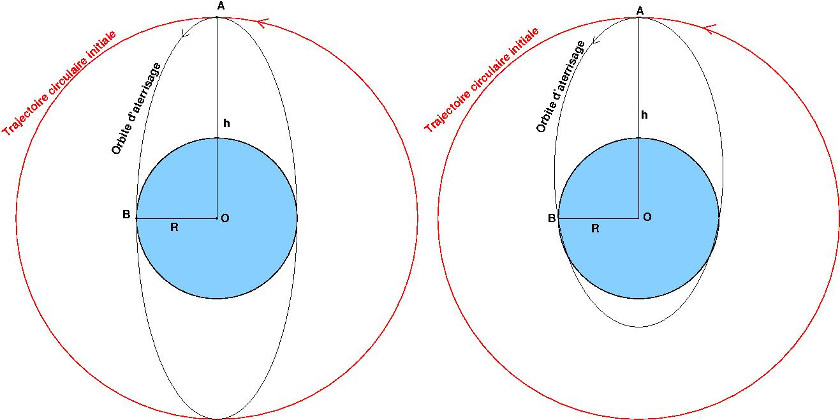
Voici deux schémas qui vont peut-être t'aider.
Bien sûr, seule la partie de l'ellipse avant l'intersection avec la surface de la terre a un sens physique !
Attention : celle de gauche, a priori plus simple (on exclut j'imagine les problèmes liés à l'entrée dans l'atmosphère terrestre...), ne peut en aucun cas être obtenue ! Saurais-tu expliquer pourquoi ?
Pour les calculs, les pistes sont nombreuses : conservation de l'énergie, conservation du moment cinétique au point O, équation paramétrique de l'ellipse, formules de Binet...
Bonjour
Merci a vous 2 d'avoir répondu ! Krinn ma question etait comment demontrer par les calculs la trajectoire elliptique du satellite ? J'ai essayé le pfd mais ne donne rien. Vanoise, la trajectoire est bien elliptique et correspond au schema de droite et non de gauche car la terre doit etre l'un des 2 foyer de l'ellipse et non le centre de l'ellipse. Cest bien ca? Par contre vanoise, pour les calculs, la conservation de l'energie mecanique me donne seulement la vitesse :
Em(A)=Em(B)
1/2mv^2-GmM/h=0-mgr
Ce qui donne v
Mais comment obtenir l'equation de l'ellipse s'il vous plait ? Calculer son excentricité etc ?
Bien vu en ce qui concerne la figure de gauche !
Pour les caractéristiques de l'ellipse : l'équation de l'ellipse en coordonnées polaires (r, ), faisant intervenir cos(
), faisant intervenir cos( ), l'excentricité e et le paramètre p est-elle connue ? Si oui, écrire que les point A et B appartiennent à cette ellipse permet d'obtenir e et p de façon quasi immédiate. Pour la vitesse Vo lors du mouvement circulaire, la RFD donne directement le résultat. Pour la vitesse VA en A, juste après le freinage, on peut y arriver en combinant la RFD et les équations de Binet qui doivent avoir été vues en cours.
), l'excentricité e et le paramètre p est-elle connue ? Si oui, écrire que les point A et B appartiennent à cette ellipse permet d'obtenir e et p de façon quasi immédiate. Pour la vitesse Vo lors du mouvement circulaire, la RFD donne directement le résultat. Pour la vitesse VA en A, juste après le freinage, on peut y arriver en combinant la RFD et les équations de Binet qui doivent avoir été vues en cours.
Tu as raison pour la vitesse en B : il faut raisonner sur la conservation de l'énergie mécanique.
Remarque : attention au notation : dans ta solution proposée, tu utilises avec pertinence l'expression de l'énergie potentielle faisant intervenir la constante universelle de gravitation G et la masse M de la terre mais j'ai crû comprendre que l'énoncé utilise g : intensité de la pesanteur à l'altitude nulle. Il faut harmoniser les notations même si l'utilisation de g est moins rigoureuse : cela conduit à confondre champ de gravitation et champ de pesanteur mais l'erreur relative est assez faible.
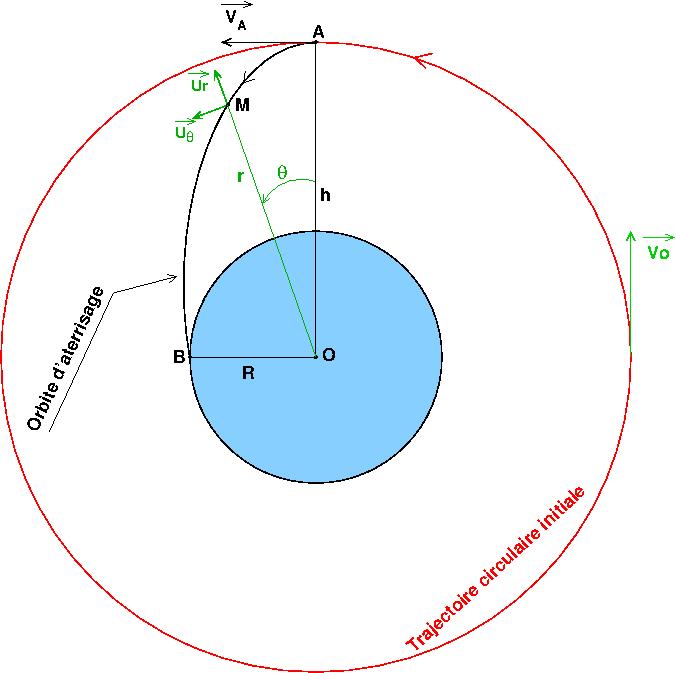
Puisque la figure de gauche est éliminée, voici celle de droite avec la définition des coordonnées polaires (r, ). Ur et U
). Ur et U sont deux vecteurs unitaires
sont deux vecteurs unitaires
comment demontrer par les calculs la trajectoire elliptique du satellite ?
- pour le démontrer il faut reprendre ton cours: tu peux partir de l'expression de l'énergie mécanique Em en fct de l'excentricité
ici Em <0 donc e<1 => trajectoire elliptique
cf
- d'autre part, si j'ai bien compris l'exo, on te demande la vitesse en A pour que la nouvelle trajectoire (théorique) soit l'ellipse de droite sur le croquis, mais sur cette nouvelle trajectoire (théorique) la vitesse n'est pas nulle en B.
il faudra une autre phase de freinage (dont on ne s'occupe pas ici) pour vraiment atterrir en B, et durant cette phase Em ne se conservera pas
Merci Vanoise et Krinn pour votre reponse. Vanoise, l'excentricité et le parametre ne sont pas connu, mais le corrigé en parle sans demontrer quoique ce soit. Jaimerai moi meme retrouver les resultats ! Mais comment faire ? Si A et B appartiennent a l'ellipse, on peut ecrire: A et B sont tQ:
x^2/a^2+y^2/b^2=1 avec a le grand demi axe,b le petit demi axe. Comment trouver e et p? On les a pas vu mais le corrigé en parle et donne juste le resultat final, ce que j'aimerai quand meme retrouver.
Pour la vitesse: Les formules de Binet me sont inconnues, on les a pas vu, je pense qu'il y a surement un moyen de resoudre l'exo sans meme si je ne vois pas encore comment.
Pour la notation de G et g: Du coup j'ecrirai -mgh en A et non -GMm/h ?
Krinn
N'ayant pas vu ce resultat en cours et en consultant ton lien sur wikipedia, il me suffirait donc que de demontrer que Em<0 ? Pour avoir une trajectoire elliptique ?
Dans ce cas, je dois raisonner avec Ec et Ep ?
De plus, pour la vitesse en A, avant freinage, on aura Va=(GMterre/h)^1/2 et apres freinage comment retrouver v? Surtout supposer la conservation de Em est elle faux? Pour le point tu predis l'existence d'une autre phase dont on s'en occupe pas ici, mais si on s'en occupe pas ici, ne peut on pas supposer qu'elle n'existe pas ? D'autant plus que l'enonce precise bien le satellite atterit en B, du coup negliger Vb est ce faux ??
Pour la notation de G et g: Du coup j'ecrirai -mgh en A et non -GMm/h
Pas du tout ! L'altitude du satellite est trop importante pour cela !
En confondant force de pesanteur et force de gravitation, on peut écrire à l'altitude nulle : m.g = G.M.m/R2 ; Le produit G.M que tu utilises correctement peut, si l'énoncé le demande, être remplacé par g.R2 ; je t'ai déjà expliqué que cette notation n'était pas très rigoureuse.
Pour l'équation polaire d'une conique, tu peux regarder le lien suivant :
Pour démontrer que la trajectoire sous l'action d'une force de gravitation est une conique, il faut combiner le PFD et la seconde équation de Binet.
Pour démontrer que la conique est une ellipse, suit la méthode et le lien indiqué par krinn ; mais la démonstration utilise la première formule de Binet !
Je ne comprends pas comment tu te retrouves avec un tel exercice sans avoir démontré au préalable les deux formules de Binet !
Tu vas sûrement en trouver une démonstration sur le net. Si cela ne te conviens pas, demande de l'aide !
N'ayant pas vu ce resultat en cours et en consultant ton lien sur wikipedia, il me suffirait donc que de demontrer que Em<0 ? Pour avoir une trajectoire elliptique ?
comme je l'ai dit au tout début, il suffit à mon avis de dire que VA < vitesse de libération en A pour démontrer que la trajectoire est elliptique
mais comme tu ne semblais pas convaincu, je t'ai indiqué une autre voie pour le montrer (mais qui suppose de très bien connaitre le cours: formules de Binet etc.)
De plus, pour la vitesse en A, avant freinage, on aura Va=(GMterre/h)^1/2 et apres freinage comment retrouver v?
on connait la nouvelle trajectoire, on connait les paramètres de l'ellipse: p et e donc a (cf mon lien)
et donc Em , puisque Em = -GMm/2a (dans le cas d'une trajectoire elliptique)
et comme Em = Cste = -GMm/r + 1/2 mv2 en tout point de la trajectoire, on en déduit VA après le freinage
(pour démontrer que Em ne dépend que de a, cf mon lien)
il est clair que cet exo demande une bonne maitrise du mvt képlérien
Vanoise, effectivement merci pour cette égalité assez astucieuse du coup jaurai juste a remplacer GM par gR^2 meme si c'est assez approximatif comme tu l'as deja rappellé ! Par contre, non je n'ai pas vu les formules de Binet en cours, pas au programme sans doute et l'exercice a l'air d'être assez ancien et doit etre sans doute de l'ancien programme! Mais merci pour ton aide ! du coup sans binet pas d'autre moyen ?
Krinn, il m'est difficile de demontrer Em=-GMm/2a car il semble que cela traite des coordonnées polaires d'une conique(indique dans le lien) chose que j'ai pas encore vu ! Du coup sais tu si il y a un autre moyen de resoudre cet exercice notamment pour la nouvelle vitesse apres freinage du satellite ? Je pense notamment a une hypothese de l'exercice fondamental qu'on a pas utilisé !
Pour la 1ere partie, Va< Vliberation me parait trop approximatif et sans t'offenser pas rigoureux, rien ne prouve que cette nouvelle trajectoire soit elliptique et non parabolique etc... Mais si il n'y a pas d'autres moyen de passer par les coordonnées polaires d'une conique et les formules de Binet, je pense que on sera obligé de faire cette supposition.
Merci a toi en tout cas ! Cet exercice me prenait la tete !
Va< Vliberation me parait trop approximatif et sans t'offenser pas rigoureux,
c'est on ne peut plus rigoureux, (re)lis ton cours
tu verras que si v < Vlibération la trajectoire est alors fermée (ellipse) - ça correspond à Em<0 -
sinon le satellite part à l'infini (il n'est pas lié à l'astre, il a assez d'énergie pour se "libérer" de l'attraction de l'astre)
Krinn dans le cours, on avait traité Em<0 implique la planete est dans un etat lié et non en diffusion et est effectivement inscrite dans une trajectoire elliptique mais on venait juste de traiter les 3 lois de kepler, et il s'agissait de la trajectoire des planetes autour du soleil. Ici est il legitime de comparer la terre avec le soleil et le satellite avec la terre ?
ici on traite un problème à 2 corps dont un de masse très faible par rapport à l'autre
les résultats s'appliquent que ces corps soient le soleil et la terre, ou la terre et un satellite, ou encore
le soleil et une comète, etc.
c'est le rapport des masses qui importent
D'accord !! Merci pour ton aide Krinn !! En effet, Em<0 dit absolument tout ! du coup pour la nouvelle vitesse apres freinage:
1/2mv^2-gh=0-mgR est ce possible ?
attention, ici il faut prendre la vraie expression de Ep: Ep= -GMm/r
l'approximation Ep=mgz n'est pas valable en A
d'autre part, comme je l'ai déjà dit, sur la nouvelle trajectoire elliptique VB n'est pas nulle
Selon toi : 1/2mVa^2-GM/h=1/2mVb^2-mgR cest ca ?
Comment fait on si Vb=!0 ? Comme je l'ai deja rappellé, l'énoncé precise bien, le satellite atterrit en B.
on aurait: 1/2mVa^2-GMm/h = 1/2mVb^2-GMm/R si la trajectoire réelle était la branche d'ellipse AB (auquel cas le satelite s'écraserait)
si la vitesse est nulle en B alors il y a forcément dissipation d'énergie entre A et B et Em ne se conserve donc pas
l'énoncé est plus subtil que ça:
En un point A un pilote declenche une poussée retrograde pendant un temps tres court de telle facon qu'il PUISSE aterrir en un point B de la terre
on ne s'occupe ici que de la modification de l'orbite en A, pas de la phase de freinage ultérieure dans l'atmosphère terrestre
A partir du dessin pas à l'échelle :
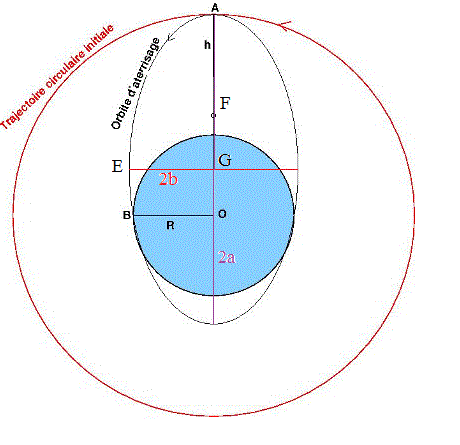
Soit 2a la mesure du grand axe de l'ellipse trajectoire (après le "coup de frein").
et 2b la mesure du petit axe de l'ellipse trajectoire.
O est bien entendu un foyer de l'ellipse.
Soit F le second foyer.
OB = AF = 2a-h
OF = 2a-2(2a-h)
OF = 2h-2a (distance entre les 2 foyers)
Pythagore sans le triangle BOF : R² + OF² = BF²
BF = V[R² + (2h-2a)²]
OB + BF = 2a (de la définition d'une ellipse)
R + V[R² + (2h-2a)²] = 2a
V[R² + (2h-2a)²] = 2a - R
R² + (2h-2a)² = (2a-R)²
R² + 4h² + 4a² - 8ah = 4a² + R² - 4aR
4h² - 8ah = - 4aR
h² = 2ah - aR = 0
a = h²/(2h-R)
La dimension du grand axe de l'ellipse est 2a = 2h²/(2h-R)
OF = 2h - 2a = 2h - 2h²/(2h-R)
OF = 2.(h²-hR)/(2h-R)
Pythagore dans le triangle OGE :
OE² = EG² + OG²
Or OE = a (propriété d'une ellipse) , EG = b
et OG = OF/2 = h-a
--->
a² = b² + (h-a)²
b² = a² - (h-a)²
b² = a² - (h - h²/(2h-R))²
b² = h^4/(2h-R)² - (2h²-hR-h²)²/(2h-R)²
b² = h^4/(2h-R)² - (h²-hR)²/(2h-R)²
b² = (h^4-h^4-h²R²+2h³R)/(2h-R)²
b² = h²R.(2h-R)/(2h-R)²
b² = h²R/(2h-R)
b = h * V[R/(2h-R)]
La dimension du petit axe de l'ellipse est 2b = 2h * V[R/(2h-R)]
L'ellipse est donc unique (pour un h donné), son grand axe est 2a = h²/(2h-R) et son petit axe est 2b = 2h * V[R/(2h-R)]
-----
Sauf distraction. (calculs non vérifiés) 
Bizarre : le schéma de J-P me rappelle quelque chose...
Pour les caractéristiques de l'ellipse, la méthode exposée par krinn et moi-même conduit directement à :
r = p/(1-e.cos( )) ; (signe "-" car l'origine en A correspond à l'apogée de la trajectoire et non au périgée comme habituellement ; (notations de mon schéma posté le 25 à 17h51))
)) ; (signe "-" car l'origine en A correspond à l'apogée de la trajectoire et non au périgée comme habituellement ; (notations de mon schéma posté le 25 à 17h51))
En A : r = h et  =0 ; donc : h = p/(1-e)
=0 ; donc : h = p/(1-e)
En B : r = R et  =
= /2 ; donc : p = R.
/2 ; donc : p = R.
L'ellipse est donc parfaitement déterminée par les deux grandeurs :
p = R ; e = 1 -R/h.
Pour la vitesse en A, krinn a indiqué une méthode très rapide qui suppose connue l'expression de l'énergie mécanique en fonction du demi grand axe a. Sinon, comme je l'ai déjà écrit, on peut combiner le PFD et la seconde relation de Binet appliquée en A juste après le freinage.
A chacun sa tactique. 
Dans ma démo, j'ai juste utilisé la définition d'une ellipse (la somme des distances d'un point de l'ellipse aux 2 foyers = constante)
et aussi le théorème de Pythagore
Cela mêne directement à la solution (trouver les caractéristiques de l'ellipse) sans aucune autre connaissance.
Cette méthode est aussi extrêmement courte, sa "longueur" ressentie en lisant ma réponse vient du fait que chaque calcul à été très détaillé pour éviter des sous-questions telles que, comment passes-tu de la ligne 5 à la ligne 6 ...
A partir de ma réponse, on peut calculer l'excentricité de l'ellipse (bien que ce ne soit pas utile avec cette méthode)
On trouverait : e = OF/2a = (2h-2a)/(2a) = h/a - 1 = (2h - R)/h -1 = 1 - R/h
Pour la vitesse en A (pour l'ellipse) : - mMG/(2a) = 1/2.m.VA² - mMG/h (conservation de l'énergie mécanique)
2.MG/h - MG/a = VA²
2.MG/h - MG*(2h-R)/h² = VA²
VA = (1/h) * RC[MGR]
Et VB par : - mMG/(2a) = 1/2.m.VB² - mMG/R
...
Toujours sans aucun calcul vérifiés.

@ Tyrion :
J'ai retrouvé un fichier destiné au départ à des étudiants de niveau bac+2 et plus pour les aider dans leurs révisions du programme de bac+1. J'ai apporté quelques modifications en fonction des questions de cours que tu te posais. Ce fichier n'a pas la prétention de remplacer un cours structuré sur le sujet mais il pourra peut-être t'aider...
Bon courage !
![]()


