Inscription / Connexion Nouveau Sujet
Trajectoire elliptique (méca')
Salut tout le monde!! 
J'ai un p'tit souci avec mon exo' de physiique, merci de bien vouloir m'aider... ^^
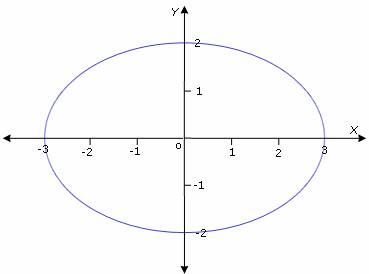
Enoncé : Le mvt du satelllite autour de la terre est elliptique. Ce mvt est décrit par les équations paramétriques
x = a cos(w.t) et y = b cos(w.t) (lire oméga au lieu de "w"  )
)
On précise que a et b sont strictement positifs.
La première question me demande de trouver une équation de la trajectoire en coordonnées cartésiennes...
Du coup j'ai trouvé que (mais c'est parce que je savais le résultat, par contre je ne sais pas si on est censé le savoir pour traiter l'exo, car au pire j'peux le montrer je dis que cos(x)^2 + sin(x)^2 = 1, et je peux en déduire aisément ce que j'ai écrit ...
Pouvez vous m'aider sur ce point ?
merci d'avance.
bonsoir,
car au pire j'peux le montrer
pourquoi "au pire" ? en 'Sup, on te demande de démontrer les résultats, pas de les deviner.
mais là c'est immédiat, comme tu l'as remarqué.
(x/a) 2 + (y/b) 2 = cos2 wt + sin2 wt = 1
Ok. 
Par contre, je ne comprends pas la question suivante ... on me demande à quels instants t, la trajectoire est plus proche de la position (0,0). Il est où le point (0,0) sur une ellipse ? Et, je ne vois pas comment utiliser mon équation de trajectoire en fait...
Ne me donne pas la réponse, mais juste des pistes de réflexions stp. 
(0,0) c'est l'origine O du repère (Ox,Oy), non ? 
et ton ellipse a pour équation dans ce repère: (x/a) 2 + (y/b) 2 = 1
ou encore la représentation paramétrique suivante:
x = a cos(w.t)
y = b cos(w.t)
Merci de me redonner mes hypothèses 
Non, en fait, moi j'avais pensé qu'on aurait pu dire que cos(w.t) = 0 et sin(wt) = 0 (mais ça c'est jamais possible ...). J'crois que je visualise mal la situation en fait ...
J'crois que je visualise mal la situation en fait ...
oui, fais un croquis et tu verras que O ne fait pas partie de l'ellipse.
mais non, tu restes sur l'ellipse (la trajectoire, c'est l'ellipse)
et on te demande le (ou les points) de l'ellipse le plus proche de O
(si j'ai bien compris)
Ah! mais non, c'est seulement quand y vaut 0, car c'est "applati dans ce sens" ... (est ce toujours le cas soit dit en passant ?)
normalement a est le demi grand axe, donc a> b
et les points cherchés sont les points M de l'ellipse vérifiant x(M) =0 y(M) = +/- b
Ah...ben oui..^^
Du coup, on a que cos(wt) = 0 et sin(wt) = 1 (ici on traite le cas y(M) = b).
Donc wt = (Pi)/2 d'ou t = (Pi)/(2w) ? (raisonnement similaire pour -b, mais cette fois avec un moins ...)
non, il y a une infinité de solutions
cos(w.t) = 0  w.t =
w.t =  /2 + k
/2 + k  k entier
k entier
(et si cos wt = 0 alors forcément sin wt = +/- 1)
où est le problème: le mouvement du satellite est décrit par la loi horaire:
x = a cos(w.t)
y = b sin(w.t)
la trajectoire est donc une ellipse. Je suppose que a > b
si M est la position du satellite à l'instant t, la distance OM est minimale quand
x=0
donc
cos wt = 0
donc w.t =  /2 + k
/2 + k k entier
k entier
donc t = ...
D'ailleurs, si c'est t minimum il y a besoin de prendre en compte l'infinité de solutions, juste la première nn ?
ce n'est pas ce que tu as demandé!
on me demande à quels instants t, la trajectoire est plus proche de la position (0,0).
maintenant si tu veux l'instant du premier passage au minimum, alors il faut faire k=0
et tu le trouves.