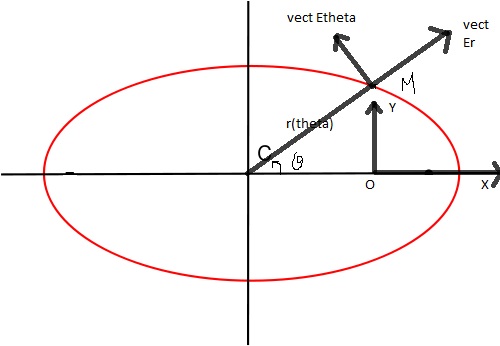
Une telle équation polaire définit une ellipse dans un repère dont l'origine est l'un des foyers de l'ellipse et l'axe est l'axe focal de l'ellipse.

euh oui , intéressant comme réponse .
j'aimerai bien savoir ou on placera les deux points =0/ .

Si le point O est un foyer de l'ellipse, l'angle est celui que fait le segment OM avec l'axe focal.
Le point de l'ellipse correspondant à = 0 est donc le point à l'extrémité droite de cet axe, où la longueur de OM est minimale (périhélie); le point correspondant à = est situé à l'extrémité gauche dudit axe (c'est le grand axe de l'ellipse) et la longueur de OM y est maximale (aphélie).

r =p/(1+e.cos(theta))
e,p=cte > 0 , 0 <= e < 1

theta = 0 ---> r min = p/(1 + e)
theta = Pi ---> r max = p/(1 - e)

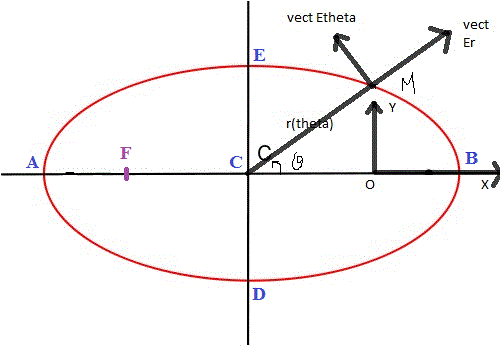
FC = CO
OB = AF

OE + OF = 2.p/(1 - e)
OE = OF -->
OE = p.(1-e)

EC = p/(1 + e)

OE² = OC² + EC²
p²/(1-e)² = OC² + p²/(1 + e)²
OC² = p²(1 + e² + 2e - (1 + e² - 2e))/[(1-e)²(1+e)²]
OC² = 4p².e/((1-e)²(1+e)²)

|OC| = 2p * V[e/((1-e)²(1+e)²)]
Avec V pour racine carrée.

Et donc avec les axes dessinés, on a, en coordonnées cartésiennes :

O(0 ; 0)
C(-2p * V[e/((1-e)²(1+e)²)] ; 0)
F(-4p * V[e/((1-e)²(1+e)²)] ; 0)

B(r max - |OC| ; 0)
A(-r max - |OC| : 0)

E(0 ; r min)
D(0 ; -r min)

Et donc, en connaissant p et e, on peut calculer les coordonnées de A , F , C , O , B , E et D.

Sachant que si M est un point de l'ellipse, on a |OM| + |FM| = 2 r max, on peut construire l'ellipse.
-----

Sauf distraction, je n'ai rien vérifié, à toi de le faire.

Priam , en prenant en considération ce que vous avez dit , les deux points seront ils placés comme suit :/?
J-P : a vrai dire , qd j'ai vu les calculs , j'ai consenti qu'il faut absolument revenir a mon cahier de cours de MAth ( Conique ) , et je le ferai ^^" .
il s'agit d'une simple question dans un exo de physique ,qui ne nécessite pas du calcul , juste un tit dessin .
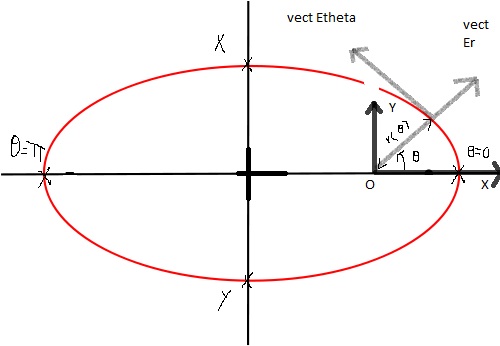
ce qui m'irrite , c'est que qd je vois la solution je trouve que les deux points correspondants a theta=0/pi sont placés X , Y (sur le schéma )
MErci bien pr vos réponses c'était intéressant ^^

C'est peut-être parce qu'il y a confusion de ma part ou peut -être pas ?

Les axes Oxy sur le dessin ont une origine qui est différente du centre de l'ellipse.

Est-ce que theta est mesuré comme sur le dessin ou bien avec le sommet de theta en O (foyer de l'ellipse) ?

Il n'est pas habituel de changer d'origine en passant de polaire en cartésien.

Si une comète à une trajectoire elliptique, son astre parent est à un foyer de l'ellipse (donc en O par exemple sur le dessin).
-----

Si theta était mesuré comme sur le dessin, le distance |CM| serait la même pour theta = 0 et pour theta = Pi

Or ce n'est pas le cas à partir de l'équation r =p/(1+e.cos(theta)).

Il me semblait donc que le sommet de l'angle theta devait être en O et pas en C sur le dessin.

C'est évidemment la première chose à tirer au clair avant d'essayer de répondre à l'exercice.

A voila, je n'avais pas vu ton dernier message.

Pour moi, theta est bien mesuré comme sur ton dernier dessin.

Mraimou, ta dernière figure est correcte.