Inscription / Connexion Nouveau Sujet
Trajectoire elliptique
Bonjour,
On a une particule M qui se déplace le long d'une courbe définie dans un repère Oxyz.
Les équations sont : x(t) = 2a.cos(2wt)
y(t) = 4a.sin(2wt)
On me demande de tracer l'allure de la trajectoire dans le plan oxy et de montrer que la trajectoire de M est bien une ellipse. On prend a= 1cm et w =1rad/s. On donnera les valeurs des demi-axes de l'ellipse.
J'ai essayé de tracer pour t=0,t=1,t=2,t=3 mais j'obtiens un truc chelou et pas du tout comme la correction du prof 
(j'ai bien mis ma calculatrice en radians)
Et comment montrer que c'est bien une ellipse svp?
Merci à celui qui m'aidera
Bonjour :
Une idée pour commencer :
Or : tu connais surement l'équation cartésienne d'une ellipse...
x2/a2 + y2/b2 =1 , a le demi-grand axe et b le demi-petit axe
Donc cos2(2wt) = x2/a2
Et sin2(2wt) = y2/b2
Donc x(t) = 2x
y(t) = 4ay/b ?
Donc x(t) = 2x
y(t) = 4ay/b ?
x(t) est une notation usuelle pour préciser que l'abscisse x varie en fonction du temps. x et x(t) : c'est la même chose ! idem pour y et y(t). En tenant compte de la relation trigonométrique fournie :
Puisque la lettre “a” est utilisée par l'énoncé, tu peux noter A et B les demis axes et écrire l'équation générale sous la forme :
Tu n'as plus qu'à identifier et continuer...
Merci Vanoise,
Je trouve A = 2a qui est le demi-grand axe et B = 4a qui est le demi-petit axe ?
Mais alors pour tracer la trajectoire je m'aidera des demi-axes? Comment je fais :/
D'accord avec tes valeur de A et B mais attention : contrairement à la situation la plus courante, le grand axe est l'axe des ordonnées. De nombreux logiciels permettent le tracé ; un simple tableur peut faire l'affaire. Sinon : place quelques points à la main et termine à "main-levée".
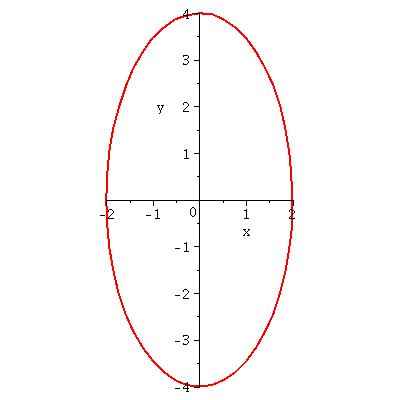
Le grand axe est toujours l'axe des ordonnées?
Pour le tracer à main levée je m'aide des équations x(t) et y(t) et je le fais pour t = 1s puis t =4s par exemple?
Et merci pour la photo !
Souvent, dans les cours de maths : A>B : la demie longueur du grand axe est donc A, la demie longueur du petit axe est B.
Ici : B>A : B désigne donc la demie longueur du grand axe qui est selon l'axe des ordonnées et A désigne la demie longueur du petit axe qui est selon (Ox). Juste une question de notation !
Pour le tracé à la main : tu peux prendre successivement les cas particuliers :
(en radians)
Un grand merci à toi!
Une dernière question, pour trouver le temps mis par la particule pour faire un tour complet, je dois montrer que x(t) et y(t) sont périodiques de 2
et faire 2wT=k2 et en déduire T?
Annuler
connectez vous