Inscription / Connexion Nouveau Sujet
Trajectoire d'un point fixe d'un segment
Bonjour, j'ai un exercice qui me pose soucis...
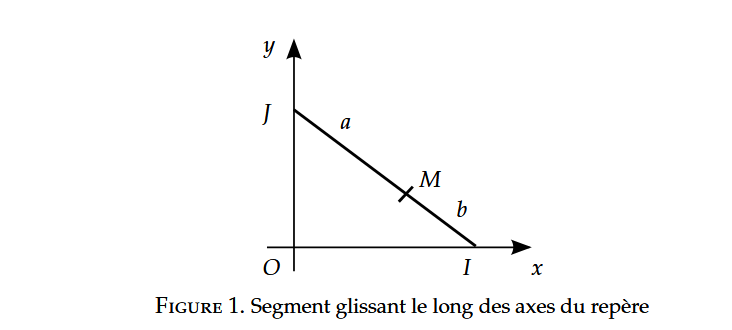
Soit a≥b≥0. On considère la courbe (C) décrite par le point M appartenant à une tige dont les extrémités Iet J se déplacent le long des axes (O,x) et (O,y), comme représenté figure 1.
1 .Donner une représentation paramétrique de (C).
2 .Donner l'équation cartésienne de (C).
3 .Tracer (C).
Je bloque dès la première question. Je ne vois pas comment trouver les fonctions pour la représentation paramétrique...
Je vous joins la figure
Bonjour
Tu peux exprimer les coordonnées cartésiennes du point en fonction de l'angle entre la tige et un axe.
Bonjour,
en attendant le retour de vanoise que je salue
comme suggéré par vanoise , soient
exprime et
en fonction de
Non, navré je vois toujours pas.
Je vois comment faire pour exprimer OI : cos  * [a+b]. Et OJ: sin
* [a+b]. Et OJ: sin * [a+b] mais pas pour x,y de M.
* [a+b] mais pas pour x,y de M.
Je garde ta définition de  . Trace une parallèle à (Ox) passant par M et une parallèle à (Oy) passant par M. Tu devrais très facilement arriver à démontrer :
. Trace une parallèle à (Ox) passant par M et une parallèle à (Oy) passant par M. Tu devrais très facilement arriver à démontrer :
x=a.cos( )
)
y=b.sin( )
)
Pour la question 2, il faut éliminer le paramètre  de la façon la plus "classique" qui soit : tu connais sûrement la relation entre les carrés du sinus et du cosinus d'un même angle.
de la façon la plus "classique" qui soit : tu connais sûrement la relation entre les carrés du sinus et du cosinus d'un même angle.
Il faut traiter à part les cas a=0 et b=0.
Si a=0 : b=L : longueur de la tige. Le point M est confondu avec le point I, il décrit un segment de droite de longueur b=L le long de l'axe (Oy).
Si b=0 : a=L. Le point M est confondu avec le point J, il décrit un segment de droite de longueur a=L le long de l'axe (Ox).
Sinon, la relation entre le sinus et le cosinus que tu as écrite te fournit l'équation cartésienne de la trajectoire de M.

 cos
cos
