Inscription / Connexion Nouveau Sujet
Tracer diagramme V(x) et M(x)
 leprof001
leprof001Bonjour
Voici une présentation où q = 500 daN:
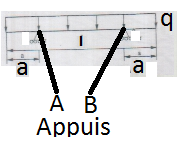
Je dois calculer les reactions d'appuis avec les parametres (a) et (l). Avec ces variables je dois tracer les diagrammes V(x) et M(x).
Voici ce que j'ai fais :
Soit Ra et Rb les reaction respectivement en A et en B
J'ai trouvé :
Ra = 250l Newtons
Rb = 250l Newtons
Pour calculer les sollicitations j'ai fais 3 coupures :
1ere coupure de 0 à a
T(x) = -500x
M(x) = -250x2
2eme coupure entre a et l-a
T(x) = -500x+Ra
M(x) = -250x2+Ra(x-a)
3eme coupe entre l-a et l
T(x) = -500x+Ra+Rb
L'expression du moment me cause des difficultés en raison du fait que je n'arrive pas à trouver la valeur entre vecteur Rb et l'axe passant par le coupure.
Maintenant quand j'aurai déterminé cela comment représenter les diagrammes alors qu'il y a a et l. Mais je veux partir du principe que l=x*a. Dois je utiliser ce principe ?
Merci de votre aide
Salut,
Se souvenir d'une chose : moment = force x bras de levier (au signe près)
Détermination des appuis Ra et Rb
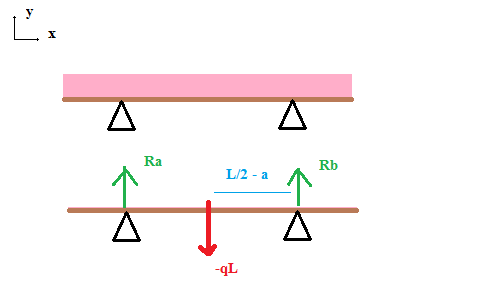
* Equation /y :
Ra + Rb - qL = 0 (1)
* Equation de moment en A / z :
- (L/A - a)*(-q.L) + (L-2a)*Rb = 0 (2)
Par résolution du système d'équations :
(2) => Rb = (L/A - a)*(-q.L)/(L-2a)
valeur qu'on injecte dans (1) pour avoir Rb.
On a donc Ra et Rb.
Je vais te proposer une méthode simple de détermination de tes équations sur chaque tronçon :
j'appelle ceci le "principe du scanner" : tu balayes de droite à gauche ta poutre, et dès que tu rencontres un effort nouveau --> une équation à écrire.
Ainsi, tu auras ici trois tronçons à détailler.
Et selon ton cours, le torseur de cohésion conduit au raisonnement suivant :
"+ ce qui est à droite" --> on ne regarde ce qu'il y a à droite du tronçon, puis on multiplie par "+" les relations finales ;
"- ce qui est à droite" --> on ne regarde ce qu'il y a à gauche du tronçon, puis on multiplie par "-" les relations finales ;
Tronçon 1 :
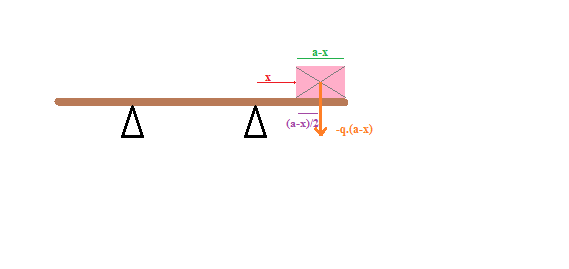
Ty = -q.(a-x)
Mfz = - (a-x)/2 * q.(a-x) = -q.(a-x)²/2
"-" --> pour le signe du moment (on va dans le sens indirect du repère)
(a-x)/2 --> bras de levier lorsqu'on regarde au niveau du tronçon en x
q.(a-x) --> valeur de la force équivalente pour le bout de tronçon considéré à droite.

Tronçon 2 :
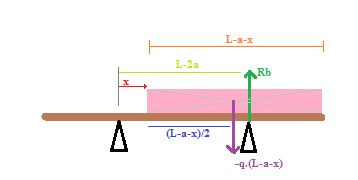
Ty = + Rb -q.(L-a-x)
Mfz = +(L-2a-x)*Rb - q(L-a-x)²/2
Je te laisse faire le troisième tronçon.
Ce n'est pas si compliqué ce type d'exercice, c'est juste long et il faut ne pas faire de faute d'inattention, ce qui est largement possible pour moi après une journée de boulot ^^
je souhaiterais que tu revois de plus pres ta résolution depuis le stade de calcul des réactions d'appuis
merci
Si tu parles de ta répartition linéaire de charge le long de la poutre, j'ai considéré q = 500 daN/m
Attends, on inverse pas les rôles, je t'ai donné des pistes.
Et pour déterminer les réactions aux appuis, tu ne peux pas t'en sortir sans poser deux équations :
* équation de la résultante statique par rapport à y
* et une équation de moment en un point judicieusement choisi : j'ai choisi A pour supprimer le moment de la réaction d'appui en ce point.
C'est ce que je t'ai écrit, à toi donc de voir si c'est OK de ton côté pour l'application numérique.