Bonsoir,

Je dois préparer un tp qui correspond à l'étude d'un ciruit RLC en régime transitoire et j'aurais besoin d'aide.

Voici l'énoncé : (les questions sont en italiques)

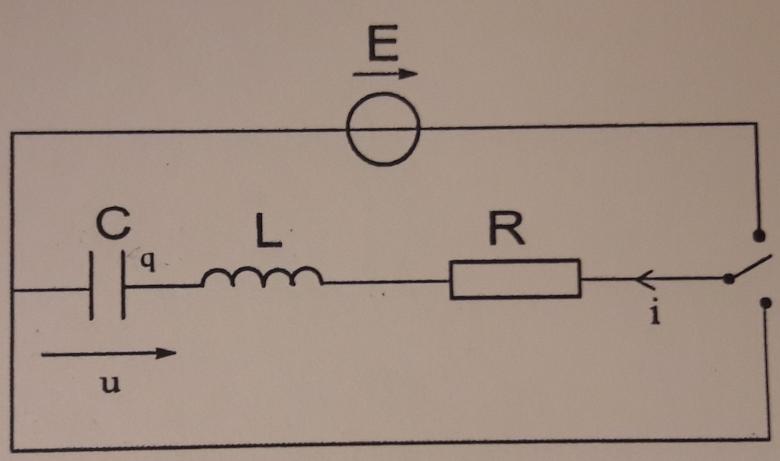
On souhaite étudier expérimentalement la tension aux bornes du condensateur d'un circuit RLC série en réfime transitoire en réponse à une tension E constante (interrupteur en position 1) ou en régime libre (interrupteur en position 2) (cf 1er schéma ci-dessous).

Matériel à disposition :
- GBF
- oscilloscope
- bobine L=100mH
- condensateur C=10nF
- Résistance variable (de 10à 100k)

1.Proposer un montage permettant de réaliser l'étude souhaitée. On précisera les branchements nécessaires, ainsi que les caractéristiques du signal choisi pour le GBF (type, fréquence, amplitude, valeur moyenne).

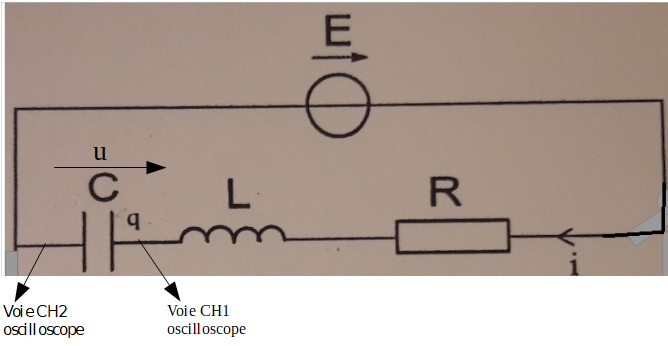
On peut faire le montage suivant : (cf schéma 2 (excusez-moi pour la mauvaise qualité de l'image))
Je ne savais pas où mettre la masse je n'ai pas vraiment compris à quoi cela sert.
Pour la fréquence et l'amplitude, je ne sais jamais comment choisir quelque chose qui "correspond" au circuit...
valeur moyenne = aire sous la courbe sur un intervalle d'une période / période
J'imagine qu'on la déterminera expérimentalement.


2. Calculer la valeur de résistance correspondant au régime critique.

Pour le régime critique on obtient u=(At+B)e^r_ot avec , et r_o=-_o/2Q=-_o car Q=1/2

On détermine B=E et A=-Er_o car on doit avoir i(0)=0 et u(0)=E.


3. Réaliser le montage et observer les tensions aux bornes du GBF et du condensateur. Faire varier la valeur de la résistance R. Décrire les observations et commenter.

Je ne sais pas encore ce qu'on observera.


Partie 2 : mesures en régime pseudo-périodiques

Choisir une valeur de résistance R=200

4. Quelles sont les valeurs du facteur de qualité de _o, de T_o, de et de T attendues ?

On a , T_o= ?  , d'où et
Je ne vois pas comment déterminer T_o


Faire une acquisition permettant de visualiser le régime transitoire de la tension aux bornes du condensateur en réponse à une tension E constante.

5. Mesurer la valeur de la pseudo-période T et commenter.
A faire expérimentalement.



On souhaite ensuite déterminer le facteur de qualité du circuit. On peut modéliser de manière mathématique l'enveloppe de la courbe obtenue précédemment.


6. Quelle est l'équation de l'enveloppe de la courbe obtenue en régime pseudo-périodique ? Proposer une méthode afin de vérifier la décroissance exponentielle telle que prédite par la théorie. Comment peut-on alors déterminer Q ?

L'équation de l'enveloppe de la courbe obtenue en régime pseudo-périodique est
Afin de vérifier la décroissance exponentielle telle que prédite par la théorie, on peut mesure l'amplitude max de la courbe en fonction du temps (l'amplitude est décroissante).
Je ne vois pas comment déterminer Q sur la courbe....

7. Réaliser l'exploitation précédemment proposée à l'aide du logiciel Regressi et commenter.
A faire expérimentalement.


Une autre méthode permettant de déterminer le facteur de qualité consiste à utiliser le décrémenet logarithmique défini par .

8. Montrer que . En déduire que si
J'ai réussi à obtenir la même formule. Si alors on peut négliger dans l'expression de d'où .

9. En déduire une valeur de Q. Commenter.
Je n'ai pas compris comment on utilisait le décrément logarithmique pour trouver Q.....


Merci d'avance pour votre aide !