Inscription / Connexion Nouveau Sujet
TP de mécanique,mouvement parabolique.
Bonjour,j'ai fais un TP de mécanique dans lequel je devais faire glisser un mobile sur une table incliné de façon à ce que sa trajectoire soit une parabole(après qu'il est rebondit sur une tige).
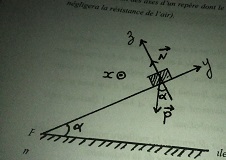
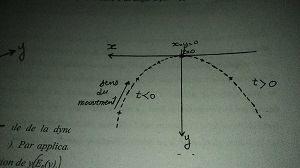
Et après avoir obtenu cette parabole sur un papier métallisé,on me demande en fonction du temps les position x,y,vx,vy, ax,ay et Ep(y).
Et j'aurai besoin d'un peu d'aide si possible,voici ce que j'ai observé et mes questions:
Pour l'instant j'ai pu calculer les vitesses pour les x positifs(voir schéma),mais je me demande si les vitesses sont négatives pour les x négatifs et si il existe vraiment des temps négatifs.
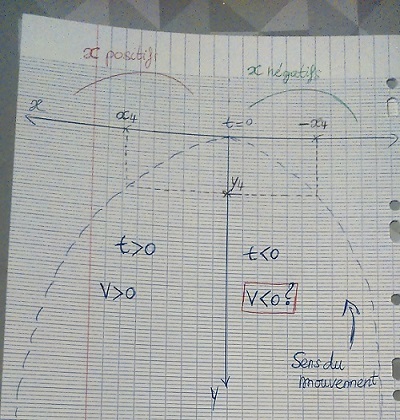
En outre,la formule que j'ai utiliser pour calculer la vitesse pour vx c'est et pour vy,
Ensuite pour ax j'utilise
Mais dans mon TP,on me proposait une formule pour la vitesse en un point qui est:
;mais ma formule avec x2,x0 me parait plus simple.
Par ailleurs,sur mon schéma,j'ai observé que sur l'axe des x,deux x opposé on la même ordonnée,et j'ai supposé que v<0 pour x négatifs.
Par ailleurs,on me dit de retrouver par application de la RFD les équations du mouvement (a,v,OM,vecteurs).
Et j'ai donc dit que:
 F=m.a=m.g=>a=g.
F=m.a=m.g=>a=g.
Puis que et
Et suite norme de v=v=
=intégral
 -g.dt=-gt+c1.
-g.dt=-gt+c1.
d'ou .
d'ou OM(vecteur)=(-gt²/2+c1t+c2).k
Mais tout ce que j'ai dit est-il bien vrai?
bonjour
quelques éléments de réponse:
je me demande si les vitesses sont négatives pour les x négatifs et si il existe vraiment des temps négatifs
qu'appelez-vous v? si c'est le module de la vitesse, v est tjs positif
quant au temps, on peut prendre l'origine des temps à l'instant que l'on veut, c'est une convention, donc des temps négatifs sont tout à fait possibles (de même que des altitudes négatives sont possibles etc.)
Par ailleurs,on me dit de retrouver par application de la RFD les équations du mouvement
attention, ce n'est pas une chute libre, il ne faut pas oublier la réaction du support!
dans R(O,x,y,z) on a: (s'il n'y a pas de frottement)
z" = N - P cos a = 0, z'=0, z=0 (le mobile est lancé de telle façon qu'il reste tjs en contact avec la table)
y" = - P sin a
x" = 0
on trouve effectivement que le mouvement est plan et que tout se passe comme si on avait une chute libre avec vitesse initiale dans laquelle on remplacerait g par g sin a (on diminue ainsi l'effet de la gravité sans changer la nature du mouvement, ce qui permet de faire des TP plus facilement)
Ce n'est pas clair pour un sou.
Que vient faire la dedans une tige sur laquelle le mobile rebondit par exemple ?
Il est tout à fait possible d'obtenir une trajectoire en parabole pour le mobile sur un plan incliné (supposé sans frottement) ... sans rebond sur quoi que ce soit.
Il suffit de lancer le mobile (vitesse initiale) sur le plan incliné, vers le haut du plan incliné mais dans une direction autre que la ligne de plus grande pente.
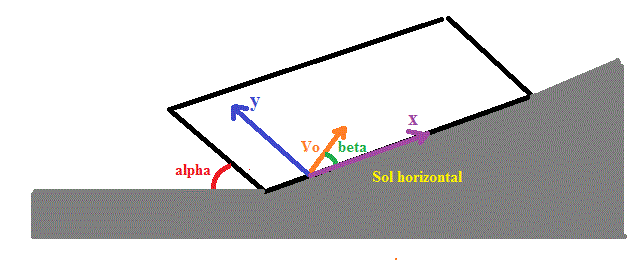
Avec le repère que j'ai dessiné :
on a :
Ax = 0 (accélération)
Ay = - g.sin(alpha)
Ce qui permet de trouver Vx(t) et Vy(t) en tenant compte des conditions initiales : Vx(0) = Vo.cos(beta)
et Vy(0) = Vo.sin(Beta)
Vx(t) = Vo.cos(beta)
Vy(t) = Vo.sin(Beta) - g.sin(alpha) * t
et d'en déduire x(t) et y(t)
x(t) = Vo.cos(beta) * t
y(t) = Vo.sin(Beta) * t - g.sin(alpha) * t²/2
-----
Reste à voir si c'est ce qui est attendu.
Sauf distraction.

qu'appelez-vous v?
C'est vrai que je n'ai pas été précis,en faite je voulais parler de vx et vy négatif du côté t<0.
Ah oui j'ai pas penser à N,je pensais que c'était nul sans frottement.
Oui on a bien ce que tu dis si z"=az,x"=ax.
Le mouvement est suivant y oui,mais c'est fou,tu a compris la même chose que ma prof (on diminue l'effet de la gravité pour faire le TP plus facilement) sans même l'avoir fait chapeau!
Merci pour ton aide

Ce n'est pas clair pour un sou.
Que vient faire la dedans une tige sur laquelle le mobile rebondit par exemple ?

c'était un élastique excuse moi) :/
Ensuite comme il est lâché sans vitesse initial donc les v0 valent 0,merci
 .
.
Mais aurai-je des vitesse vx <0 pour le cas x<0 (t<0) ? (voir mon schéma).
Je trouve ça bizarre de mettre Vx(t=-0.1s) par exemple.
Après, Vy sera toujours positif,je pose pas la question.
Mais j'aurai du écrire l'énoncé complet avant,le voici:
Lâché le mobile:il descend le plan incliné en un mouvement rectiligne et heurte l'élastique coté opposé qui le renvoi vers le haut.
Le mobile décrit une trajectoire parabolique.
Là il me reste à trouver Ep(y) par l'application du théorème de l'Ep,mais je vais chercher avant de vous poser des questions.
Merci pour votre aide à vous deux encore une fois
 .
.Je précise pour pour calculer vx pour x<0 à t<0 j'utilise ma même formule mais pour x<0;x2<x0 donc x2-x0<0 et 2T<0 aussi donc la vitesse est positive normalement.
Salut,j'ai réfléchis de nouveau sur ce tp et je l'ai traité d'une autre façon.
voici l'énoncé:
Un mobile est équipé d'une bague pour choc élastique.
mettre le moteur en marche et placer le mobile sur le côté surélevé de la table.
Orienter le mobile de sorte à ce que 2 ressort opposés de la bague soient perpendiculaires aux élastiques limitant le plan incliné à son sommet et à sa base.
Lâché le mobile:il descend le plan incliné en un mouvement rectiligne et heurte l'élastique coté opposé qui le renvoi vers le haut.
Le mobile décrit une trajectoire parabolique.
Cependant je n'ai pas trouver l'expression de Ep(y) par l'application du théorème de l'Ep.
Et j'aurai besoin d'aide pour cela si possible.
Ensuite voici un schéma pour vous permettre de mieux comprendre mon tp.
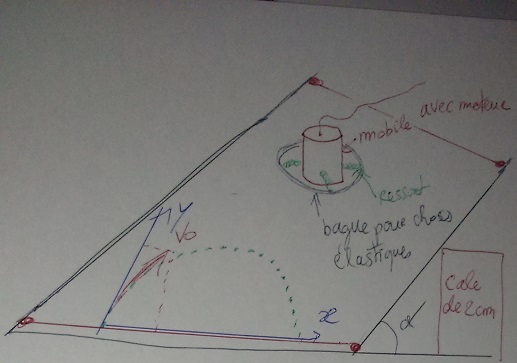
J'ai pu observer que le mouvement est parabolique est qu'il est similaire à un mouvement de chute libre ,
sauf que vu qu'on est sur un plan(plan incliné) le mouvement sera étudié sans l'axe z et toute les équation qu'on trouve pour l'axe z en chute libre,position,vitesse...sont les équations de l'axe des y.
Comme on peut le voir sur mon schéma,le mouvement est étudié selon deux axes,y et x.
Mais si je me trompe,veuillez me le dire,merci


