Inscription / Connexion Nouveau Sujet
Tonneau de Pascal
Bonjour, je n'arrive pas à comprendre le phénomène du tonneau de Pascal.
Si j'ai bien compris : On a un tonneau rempli d'eau, on crée une petit ouverture arrondie en haut du tonneau, on fait passer un tube du même diamètre que le trou dans l'ouverture et on rajoute de l'eau dans le tube.
Et apparemment, le tonneau explose, alors que la quantité d'eau rajoutée dans le tube n'est pas si grande que ça.
Ce que j'ai lu semble dire que c'est à cause de la loi de l'hydrostatique. De ce que j'ai compris de cette loi : On a un tube rempli d'eau. On prend un point A dans l'eau et un point B situé plus bas dans l'eau. La pression exercée sur B est alors "PB = PA + g  h".
h".
Pour moi, dans ce cas là ça a du sens, car " = m/V = m/(S*h)". On a ainsi "PB = PA + mg", donc, la différence de pression est due au poids du fluide contenu entre les 2 points.
= m/V = m/(S*h)". On a ainsi "PB = PA + mg", donc, la différence de pression est due au poids du fluide contenu entre les 2 points.
Là ça marche parce-que la surface "S" d'une coupe du tube est la même entre les 2 points.
Sauf que dans le 1er cas, vu que le tube qu'on met dans le tonneau a une surface nettement plus petite que la sienne, le volume d'eau ajouté (et l'ajout de pression qui va avec) devrait être insignifiant à côté de celui du tonneau.
Alors comment ça marche ?
Bonsoir
D'accord avec le début de ton message jusqu'à PB=PA + g.h
g.h
Pas d'accord avec la suite. La pression dans le tonneau dépend de h, pas directement de la masse d'eau dans celui-ci. Imagine deux tuyaux de mêmes longueurs mais de sections très différentes. Le plus gros contient beaucoup plus d'eau mais produit la même surpression dans le tonneau.
Oui j'ai bien compris que 2 tuyaux de même hauteur mais de diamètres différents produisent la même pression, seulement je n'arrive pas à me représenter comment c'est possible. Mathématiquement je le comprends, mais je peux difficilement admettre que c'est juste "comme ça".
Comment dire... je comprends bien que ça dépend de la hauteur, sauf qu'une hauteur ne provoque pas de pression (ce n'est qu'une mesure de longueur), c'est ce qu'il y a "DANS" cette hauteur qui la crée, non ?
"Comment dire... je comprends bien que ça dépend de la hauteur, sauf qu'une hauteur ne provoque pas de pression "
Un colonne d'eau de hauteur h (quelle que soit sa section) provoque une différence de pression Delta P = Rho(eau) * g * h
Donc si on a une pression Po (par exemple la pression atmosphérique) au dessus de la colonne d'eau, au bas de la colonne d'eau (donc du tuyau), on a une pression : P = Po + Rho(eau) * g * h
Exemple numérique.
Soit un tonneau de 1 m de haut qui a été remplit à ras bord par de l'eau sous pression atmosphérique et puis a été fermé. La surface du fond du tonneau est 0,5 m²
La pression au niveau du fond du tonneau est P1 = Po + Rho(eau) * g * h (avec Po la pression atmosphérique)
P1 = 100000 + 1000 * 10 * 1 = 110000 Pa
Mais la pression à l'extérieur du tonneau est Po = 100000 Pa
La force sur le fond du tonneau (de surface S) est F1 = (P1 - Po)*S
F1 = (110000 - 100000)*S = 10000*0,5 = 5000 N
Si on perce le couvercle par un petit trou et qu'on y introduit un tube (du même diamètre que le trou), supposons un tube de 2 m de haut.
Si on remplit le tube d'eau, la hauteur d'eau au dessus du fond du tonneau est H = 1 + 2 = 3 m
La pression au niveau du fond du tonneau est P2 = Po + Rho(eau) * g * H (avec Po la pression atmosphérique)
P2 = 100000 + 1000 * 10 * 3 = 130000 Pa
Mais la pression à l'extérieur du tonneau est encore de Po = 100000 Pa
La force sur le fond du tonneau (de surface S) est F2 = (P2 - Po)*S
F2 = (130000 - 100000)*S = 30000*0,5 = 15000 N
La force exercée sur le fond du tonneau a été multipliée par 3 par le simple ajout d'une masse infime d'eau dans le tuyau ...
On peut évidemment faire un raisonnement équivalent sur la paroie latérale ou sur le couvercle ...

Bonjour Ashaverus
sauf qu'une hauteur ne provoque pas de pression (ce n'est qu'une mesure de longueur)
Il ne faut pas oublier que l'eau est dans le champ de pesanteur !
Imagine un volume élémentaire d'eau parallélépipédique rectangle en équilibre dans le champ de pesanteur avec deux faces horizontales. L'absence de déplacement horizontal de cette eau permet de conclure que les forces exercées sur les quatre faces verticales se compensent deux à deux : la pression est donc la même dans un plan horizontal. Les forces exercées sur les deux faces horizontales du parallélépipède doivent compenser le poids de l'eau contenue dans le parallélépipède : la force de pression exercée sur la face inférieure est supérieure à la force exercée sur la face supérieure. La pression augmente donc avec la profondeur à cause de la pesanteur.
la force de pression exercée sur la face inférieure est supérieure à la force exercée sur la face supérieure. La pression augmente donc avec la profondeur à cause de la pesanteur.
................................ est-ce que... c'est dû au fait que la pression atmosphérique augmente à mesure qu'on s'approche du sol (et diminue à mesure qu'on monte en hauteur) ?
Je suis vraiment désolé mais j'ai tellement de mal à me le représenter.
Voyons si j'ai compris :
Soit "Po" la pression atmosphérique exercée sur la base du tonneau et "P1" la pression atmosphérique exercée sur la face supérieure du tonneau.
Comme la face supérieure est plus haute que la base, on a "Po > P1".
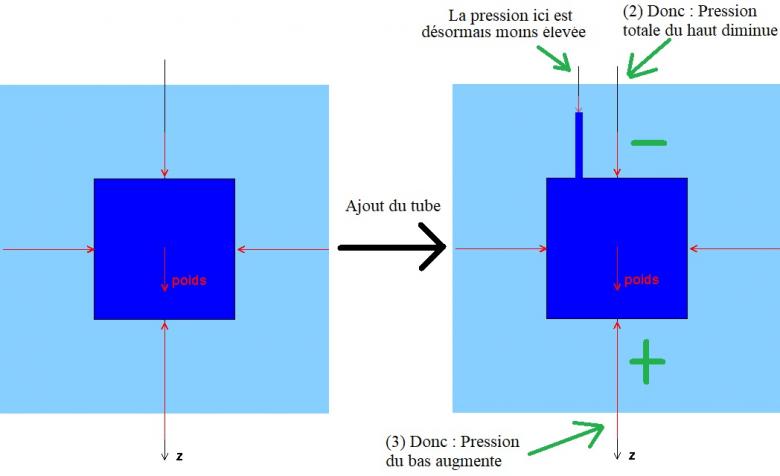
Maintenant, on perce un trou et met un tube fin sur le haut du tonneau, on remplit le tube d'eau et on le bouche. On a alors créé une nouvelle face au sommet du tube sur laquelle s'applique une pression "P2 < P1".
Le peu d'eau ajouté ne doit pas avoir eu d'influence majeure sur la pression à l'intérieur du tonneau (je suppose ?).
Bon, et là qu'est-ce qui se passe ? Quand je ferme les yeux et que j'essaie de me représenter les différentes forces, j'imagine que la pression de l'eau (intérieure) essaie de faire sortir l'eau du tonneau tandis que la pression atmosphérique (extérieure) essaie de maintenir l'eau à l'intérieur. Donc, comme la pression extérieure sur le haut du tonneau est plus faible après qu'on a mis le tube, l'eau devrait pouvoir sortir plus facilement par le haut, non ? (Quand on serre une bouteille en plastique remplie d'eau entre nos mains, si le bouchon est mal serré l'eau va sortir par là)
Tu n'as pas compris mon dernier message. J'essayais de répondre à ta phrase : "une hauteur ne provoque pas de pression". La réponse est : "mais si dans la mesure où le liquide est en équilibre dans le champ de pesanteur !".
Je reprends l'exemple de mon petit cube élémentaire de liquide, situé à l'intérieur d'un liquide de façon à avoir deux faces horizontales. Ce petit cube est en équilibre sous l'action de plusieurs forces : son poids bien sûr mais aussi les forces de pression exercées sur ce petit cube par le reste du liquide qui l'entoure. La force exercée par l'eau sur la face inférieure doit être plus grande que la force exercée par l'eau sur la face supérieure pour compenser le poids. il faut donc que la pression au niveau de la face inférieure soit plus élevée que la pression au niveau de la face supérieure. Bref : puisque le liquide doit rester en équilibre dans le champ de pesanteur, il faut bien que la pression augmente en fonction de la profondeur... C'est ce que traduit la formule de l'hydrostatique que tu connais. Fais un petit schéma pour te convaincre de cela ! Le reste est un simple calcul de pressions et de forces.
Ci-dessous : un schéma simplifié en 2D du petit cube (bleu foncé) entouré d'eau (bleu clair). J'ai représenté le poids du petit cube d'eau, deux des quatre forces de pression sur deux faces verticales qui se compensent , la force de pression exercée par l'eau sur la face inférieure, la force de pression exercée par l'eau sur la face supérieure.
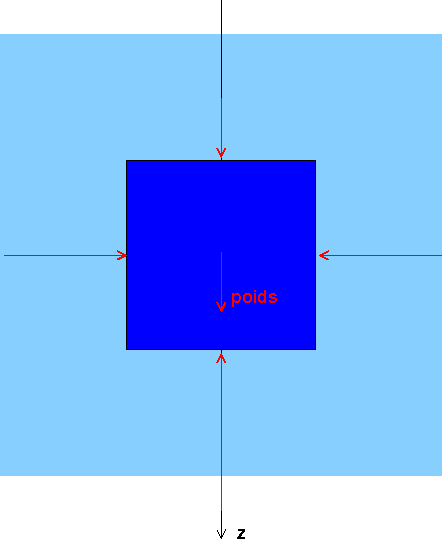
. Il faut que tu relises attentivement les messages précédents... J'ai isolé par la pensée un petit cube d'eau au milieu de l'eau en équilibre et je l'ai dessiné en bleu foncé pour le distinguer de l'eau environnante. Il faut considérer que la hauteur de ce cube est une valeur élémentaire dz... C'est en étudiant l'équilibre de ce petit cube d'eau que l'on arrive à montrer que la pression est la même dans l'eau dans tout plan horizontal et que sa variation en fonction de la profondeur z vérifie :
La démonstration se fait au niveau (bac+1).
Le but de mes deux messages précédents et de celui-ci est juste d'expliquer pourquoi la pression augmente avec la profondeur pour un fluide en équilibre dans le champ de pesanteur. Rien de plus. L'étude du tonneau de Pascal est sur la fiche dont je t'ai fourni la référence.
Oui, autant pour moi j'avais mal lu ton message.
Bon, en fait je crois que tu n'as pas compris la question que je me pose. Récapitulons :
*Que la pression dans un cylindre rempli d'eau augmente avec la profondeur, ça me semble logique : Pour le formuler avec mon vocabulaire d'amateur, "l'eau qui est au-dessus appuie sur l'eau qui est en dessous à cause de la pesanteur".
*Que la pression au fond d'un tel cylindre soit la même quel que soit son diamètre, ça aussi ça va : Je me dis que, si son diamètre est plus grand alors la quantité d'eau "appuyant" sur le fond du cylindre sera plus grande MAIS la surface sur laquelle cette eau appuie est également plus grande donc c'est normal que la pression reste la même.
*EN REVANCHE, quand on a 2 cylindres l'un sur l'autre et connectés (comme dans le cas du tonneau de pascal), que la pression sur le fond du cylindre du bas augmente de la même façon quel que soit le diamètre du cylindre du haut, ça je n'arrive pas à l'admettre .
COMPRENEZ-MOI BIEN : Ce n'est pas avec les lois, formules et calculs que j'ai un problème. C'est juste que mon "bon sens" me dit que ce n'est pas possible.
"Que le cylindre du dessus fasse 1mm, 1m ou 1km de diamètre, l'eau qui est dedans fera augmenter la pression de la base du cylindre du dessous dans les mêmes proportions", ça me semble absurde.
Est-ce que vous pourriez essayer de me l'expliquer différemment une dernière fois ?
Considère un solide indéformable. Ce solide peut transmettre des forces, pas des pressions.
Imagine maintenant l'eau au fond du tonneau. La pression de l'eau sur le fond du tonneau est partout la même si le fond du tonneau est horizontal et cela, quelle que soit l'aire de la surface du fond du tonneau. En augmentant l'aire de cette surface, tu augmentes l'intensité de la force. Tu retrouves cela aussi dans les presses hydrauliques.
"Que le cylindre du dessus fasse 1mm, 1m ou 1km de diamètre, l'eau qui est dedans fera augmenter la pression de la base du cylindre du dessous dans les mêmes proportions", ça me semble absurde.
C'est pourtant la vérité comme expliqué au début de mon message ! C'est une conséquence de la relation de la statique des fluides qui est valide en chaque point de celui-ci.
Si en tant que plongeur, tu te trouves à 10 m de profondeur dans une piscine ou bien à 10 m de profondeur dans un océan, tu es soumis à la même pression (en négligeant le sel contenu dans l'eau de l'océan)
Et pourtant la "surface" de la piscine est de très loin plus petite que la "surface" de l'océan.
Non ?
La pression hydrostatique (due à l'eau) en un endroit ne dépend que de la différence de niveau entre l'endroit considéré et la surface (haute) de l'eau.

@vanoise : D'accord. Ce n'est pas encore très clair pour moi mais je crois que je commence à voir à peu près comment ça marche, je vais prendre le temps d'y réfléchir.
@J-P : Juste pour être sûr : Donc si je suis allongé au fond de ma piscine remplie d'une hauteur "h" d'eau, et que quelqu'un prend une longue paille de hauteur 2h, place une extrémité dans l'eau et la rempli par l'autre extrémité, qu'est-ce qui se passe ?
Est-ce que la pression que je subit triple ? Est-ce que c'est différent puisque la piscine n'est pas close (et si oui qu'en est-il si on clôt le haut de la piscine en laissant juste un trou pour la paille) ?
@J-P : Juste pour être sûr : Donc si je suis allongé au fond de ma piscine remplie d'une hauteur "h" d'eau, et que quelqu'un prend une longue paille de hauteur 2h, place une extrémité dans l'eau et la rempli par l'autre extrémité, qu'est-ce qui se passe ?
Est-ce que la pression que je subit triple ? Est-ce que c'est différent puisque la piscine n'est pas close (et si oui qu'en est-il si on clôt le haut de la piscine en laissant juste un trou pour la paille) ?
Non, l'eau ne peut pas rester dans la paille dans ce cas (piscine sans "couvercle"), elle va se vider dans la piscine.
Mais si la piscine était remplie à ras bord et munie d'un couvercle étanche, le plongeur subirait bien une pression beaucoup plus grande avec la paille ...

Attention quand même :
Tu écris :
" Juste pour être sûr : Donc si je suis allongé au fond de ma piscine remplie d'une hauteur "h" d'eau, et que quelqu'un prend une longue paille de hauteur 2h, place une extrémité dans l'eau et la rempli par l'autre extrémité, qu'est-ce qui se passe ?
Est-ce que la pression que je subit triple ?"
Même avec une piscine avec couvercle, la pression sur le plongeur ne triple pas (mais elle augmente)
Sans la paille, la pression est P1 = Po + Rho.g.h (avec Po la pression atmosphérique)
Avec la paille, la pression est P2 = Po + Rho.g.(3h)
On n'a bien P2 > P1 mais on n'a pas P2 = 3 P1
-----
Par contre pour le tonneau, il y a une différence.
On aurait aussi, en remplaçant la piscine par un tonneau(avec couvercle).
Sans la paille, la pression (sur le fond) est P1 = Po + Rho.g.h (avec Po la pression atmosphérique)
Avec la paille, la pression (sur le fond) est P2 = Po + Rho.g.(3h)
Mais, dans les 2 cas, la pression extérieure au tonneau est Po (pression atmosphérique)
Et donc, le fond est soumis à une force :
F1 = (P1 - Po)*S (avec S la surface du fond.) sans la paille
F2 = (P2 - Po)*S avec la paille
F1 = Rho.g.h * S
F2 = Rho.g.3h * S
Et on a bien ici F2 = 3.F1
-----
Sauf distraction.