Niveau maths sup

TIPE résonateurs

Posté par
pepperoncino 30-07-17 à 12:56

Bonjour,

je m'intéresse dans le cadre d'un TIPE (épreuve pour les écoles d'ingénieur) à la protection acoustique des coiffe des lanceurs spatiaux. Des résonateurs sont utilisés pour absorber les basses fréquences sur Ariane par exemple. Je me suis beaucoup documentée sur le sujet, mais n'ayant que peu de notions en acoustique, je n'ai pas compris comment un résonateur peut faire office de protection acoustique, en gros pourquoi peut-on dire qu'un résonateur absorbe une onde acoustique ? Il entre en résonance à une certaine fréquence, mais comment peut-il dissiper de l'énergie ?

Merci d'avance

Posté par re : TIPE résonateurs 30-07-17 à 14:41

Bonjour
Je n'ai pas très bien compris la question...
S'agit-il de limiter la source de bruit en limitant, par exemple l'amplitude de vibrations de certaines pièces mécaniques ? Cette limitation peut se faire en couplant la pièce susceptible de vibrer (excitateur) à un résonateur (ressort + amortisseur) : si la fréquence d'excitation est éloignée de la fréquence propre du résonateur, il y a limitation de l'amplitude des vibrations de l'excitateur. On trouve sur le net de nombreuses études théorique sur ce sujet.
S'agit-il de la protection acoustique des personnes présentes sur le pas de tir compte tenu du niveau d'intensité sonore alors très important ? Il existe pour cela des casques anti-bruit dits "actif" : un microphone à l'intérieur du casque enregistre le son provenant de l'extérieur et un dispositif électronique associé à un petit haut parleur génère un son de même amplitude mais en opposition de phase ; le son résultant est ainsi d'amplitude quasi nulle.

Posté par re : TIPE résonateurs 30-07-17 à 15:00

En fait, lors de l'allumage, un champs acoustique très important est libéré par les moteurs, et cela va exciter les structures de la coiffe de la fusée. Le niveau sonore sur la paroi extérieure de la coiffe est de 183dB et les fréquences qui sont susceptibles d'endommager les structures et les charges utiles présentes sous la coiffe (satellites par exemple) sont situés dans les très basses fréquences. J'ai compris qu'une bonne solution pour absorber les basses fréquences sont les résonateurs. Donc oui il s'agit en effet de limiter l'excitation des pièces de la coiffe, là encore j'ai une confusion parce que les résonateurs sont des moyens d'absorption et non d'isolation.
En lisant une thèse sur le sujet, j'ai vu qu'il faut coupler un matériaux absorbant pour qu'il absorbe l'énergie et ne l'amplifie pas. J'ai ci-joint l'extrait que j'ai du mal à comprendre, si vous pouviez m'aider..
Merci beaucoup

TIPE résonateurs

Posté par re : TIPE résonateurs 30-07-17 à 16:20

OK Je comprends mieux ce que tu cherches. Je pense que cela n'est pas trop compliqué à modéliser. Un précision avant que je ne te réponde de façon plus adaptée : tu postes au niveau "Math Sup" ; peux-tu indiquer si tu termines ton année de math sup ou si tu rentres en math sup juste après le bac ? En cette période de l'année, la question mérite d'être posée.

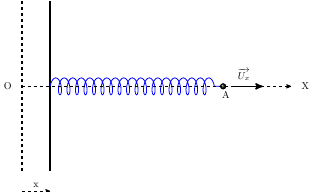
Posté par re : TIPE résonateurs 30-07-17 à 17:25

D'accord merci beaucoup.
Je passe en deuxième année en math spé, j'ai terminé mon année de sup.

Posté par re : TIPE résonateurs 30-07-17 à 21:42

Tu peux modéliser un résonateur par un oscillateur unidimensionnel constitué d'une plaque verticale plane de masse m, de surface d'aire S relié à un ressort parfait de raideur k. Je laisse de côté le résonateur de Helmholtz plus compliqué. Un dispositif de guidage non représenté sur le schéma permet à la plaque de vibrer en translation suivant un axe (Ox) horizontal en compensant le poids de la plaque. O est la position de la plaque à l'équilibre, la longueur du ressort à vide est (OA) avec A : point fixe correspondant à l'autre extrémité du ressort. On travaille dans un repère terrestre supposé galiléen et on applique la deuxième loi de Newton à la plaque. Celle-ci est soumise aux forces suivantes :

1° l'action d'une onde acoustique sinusoïdale qui exerce sur la face gauche de la plaque une surpression (appelée pression acoustique) : $p(t)=A.\cos\left(\omega.t\right)$ . L'action de l'onde acoustique se caractérise par une force :

$\overrightarrow{F}=S.p(t).\overrightarrow{u_{x}}=S.A.\cos\left(\omega.t\right).\overrightarrow{u_{x}}=F_{m}.\cos\left(\omega.t\right).\overrightarrow{u_{x}}$

2° l'action du ressort qui exerce une force de rappel :

$\overrightarrow{T}=-k.x.\overrightarrow{u_{x}}$

3° l'action d'un amortisseur qui se modélise par une force de frottement proportionnelle à la vitesse :

$\overrightarrow{f}=-\alpha.\overrightarrow{v}=-\alpha.\frac{dx}{dt}.\overrightarrow{u_{x}}=-\alpha.\dot{x}.\overrightarrow{u_{x}}\quad\alpha\text{ : constante positive}$

Deuxième loi de Newton :

$m.\overrightarrow{a}=\overrightarrow{F}+\overrightarrow{T}+\overrightarrow{f}\quad soit\quad m.\ddot{x}+\alpha.\dot{x}+k.x=F_{m}.\cos\left(\omega.t\right)$

On cherche une solution sinusoïdale (régime sinusoïdal forcé : fréquence égale à la fréquence d'excitation) :

$x=X_{m}.\cos\left(\omega.t+\varphi\right)$

Pour obtenir l'amplitude et la phase, on utilise la méthode des complexes associés comme tu as appris à le faire cette année. Demande la démonstration si tu ne t'en sors pas. Pour l'instant, je me contente de fournir le résultat concernant l'amplitude :

$X_{m}=\frac{F_{m}}{\sqrt{\left(k-m.\omega^{2}\right)^{2}+\alpha^{2}.\omega^{2}}}$

La puissance instantanée reçue par le résonateur, donc perdue par l'onde acoustique, est la puissance instantanée de la force de pression :

$P_{u}(t)=\overrightarrow{F}.\overrightarrow{v}=F_{m}.\cos\left(\omega.t\right).\dot{x}\quad avec\quad\dot{x}=-\omega.X_{m}.\sin\left(\omega.t+\varphi\right)$

Soit en tenant compte de la RFD et en remarquant : $\ddot{x}=-\omega^{2}.x$ :

$P_{u}(t)=\left(k-m.\omega^{2}\right).x.\dot{x}+\alpha.\dot{x}^{2}$

On s'intéresse maintenant à la puissance moyenne absorbée par le résonateur, c'est à dire la valeur moyenne de Pu(t) calculée sur une période. Tu as sans doute démontré en cours que la valeur moyenne sur cette durée d'un sinus ou d'un cosinus au carré vaut 1/2 alors que la valeur moyenne du produit sinus . cosinus vaut zéro. (Demande éventuellement la démonstration). On obtient ainsi une puissance moyenne absorbée :

$P_{moy}=\frac{\alpha.\omega^{2}.X_{m}^{2}}{2}=\frac{\alpha.\omega^{2}.F_{m}^{2}}{2\left[\left(k-m.\omega^{2}\right)^{2}+\alpha^{2}.\omega^{2}\right]}=\frac{\frac{F_{m}^{2}}{2\alpha}}{\left[\left(\frac{k}{\omega.\alpha}-\frac{m.\omega}{\alpha}\right)^{2}+1\right]}$

On définit la pulsation de résonance $\omega_{0}telle que : k=m.\omega_{0}^{2}$ . Pour caractériser l'acuité de la résonance on définit le facteur de qualité du résonateur :

$Q=\frac{m.\omega_{0}}{\alpha}=\frac{k}{\alpha.\omega_{0}}$

$\boxed{P_{moy}=\frac{\frac{F_{m}^{2}}{2\alpha}}{1+Q^{2}\cdot\left(\frac{\omega_{0}}{\omega}-\frac{\omega}{\omega_{0}}\right)^{2}}}$

Pour illustrer les propos de ton document, je trace d'abord (en rouge) la courbe représentant les variations de Pmoy en fonction de $x=\frac{\omega}{\omega_{0}}$ en fixant arbitrairement $\frac{F_{m}^{2}}{2\alpha}=1W$ pour une résonance assez aiguë : Q=10. Dans le même repère, je trace la courbe pour Q=2 pour des valeurs identiques de Fm, k et m, ce qui revient à multiplier par 5 la valeur de $\alpha$ et par diviser par 5 la valeur de $\frac{F_{m}^{2}}{2\alpha}$ .

Ignorant ton niveau, je me suis peut-être trop appesanti sur certains aspects en passant trop vite sur d'autres. Pose des questions si tu le juges utile.

Concernant le résonateur de Helmholtz, tu en trouveras une description sur le net ainsi que la démonstration de la fréquence de résonance. Demande de l'aide si nécessaire...

TIPE résonateurs

Posté par re : TIPE résonateurs 31-07-17 à 12:06

Bonjour,

Merci infiniment ! Votre réponse m'aide beaucoup, et surtout elle est très riche. Certains passages sont encore un peu flous, le passage à Pmoy, mais je vais m'y attarder.

Si vous avez encore un peu de temps, j'ai trouvé un autre passage de cette thèse, mais je n'ai pas les outils pour comprendre. Si vous pourriez m'aider à comprendre ces quelques lignes..

TIPE résonateurs

Posté par re : TIPE résonateurs 31-07-17 à 15:18

Citation :
Certains passages sont encore un peu flous, le passage à Pmoy, mais je vais m'y attarder.

J'ignore l'origine de tes difficultés. S'il s'agit de la démonstration de la valeur moyenne du carré d'un cosinus, j'ai été amené il y a peu à faire la démonstration sur ce forum ici :

intégralde cos² = intégrale de sin² (message du 24-07-17 à 18:20). Pour le produit sinus . cosinus, la méthode est la même.
Pour tes nouvelles questions : tu as sans doute remarqué une analogie assez forte entre l'étude des oscillations forcées ici et l'étude d'un circuit RLC série en régime sinusoïdal forcé. A la force correspond la tension en électricité, à la vitesse correspond l'intensité. Cela peut conduire à définir une impédance pour le résonateur par : $Z=\frac{F_{m}}{V_{m}}$ .

Cela est souvent posé ainsi sauf en acoustique où on préfère, pour harmoniser les deux études, définir l'impédance comme le quotient de l'amplitude de la pression acoustique sur la vitesse :

$Z=\frac{A}{V_{m}}=\frac{F_{m}}{S.V_{m}}=\frac{F_{m}}{S.\omega.X_{m}}=\frac{\sqrt{\left(k-m.\omega^{2}\right)^{2}+\alpha^{2}.\omega^{2}}}{S.\omega}$

En utilisant les notations du message précédent :

$Z=\frac{\alpha}{S}\cdot\sqrt{1+Q^{2}\cdot\left(\frac{\omega_{0}}{\omega}-\frac{\omega}{\omega_{0}}\right)^{2}}$

Cette impédance présente un minimum $Z_{min}=\frac{\alpha}{S}$ à la résonance de puissance soit pour $\omega=\omega_{0}$ (voir courbe ci-dessous tracée dans le cas Q=10 avec $\frac{\alpha}{S}=400kg.m^{-2}.s^{-1}$ .

De façon plus générale, pour une onde progressive acoustique se propageant dans l'air, l'amplitude de la pression acoustique $p_{max}=A$ et l'amplitude de la vitesse de vibration des molécules d'air $u_{max}$ sont proportionnelles. Leur quotient est l'impédance acoustique de l'air :

$Z_{air}=\frac{p_{max}}{u_{max}}\approx400kg.m^{-2}.s^{-1}$ à 20°C.

Dans mon étude d'hier, j'ai négligé un phénomène : la vibration de la plaque génère une onde acoustique dite « onde réfléchie » qui se propage dans le sens négatif de l'axe (Ox). Cette onde réfléchie transporte de l'énergie ; la puissance absorbée par le résonateur est donc dans le cas général un peu plus faible que celle calculée hier. Impossible en fin de sup de faire une démonstration rigoureuse. Il te faut admettre pour le moment que l'amplitude de l'onde réfléchie est d'autant plus faible que l'écart entre l'impédance du résonateur et celle de l'air est faible. Cela fait une bonne raison supplémentaire d'utiliser des résonateurs ayant une fréquence propre voisine de la fréquence du son à amortir. Puisque les résonateurs usuels ont en général des impédances supérieures à celle de l'air, c'est à la résonance que l'écart d'impédance est le plus faible. En pratique : le son à amortir n'est pas pur ; il résulte de la superposition de plusieurs sons de fréquences différentes ; il faut donc utiliser plusieurs résonateurs de fréquences propres différentes comme expliqué dans ton document...

TIPE résonateurs

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

TIPE résonateurs

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique