Salut,

Freinage par Courant de Foucault et forces de Laplace

Salut
Est-ce que tu peux m'aider?

Bonsoir,
J'allais te proposer le même lien que gbm.
Ce qui manque dans ce calcul, c'est effectivement d'essayer d'exprimer le résultat en fonction de (résistivité) plutôt que de R (résistance du disque). C'est que je dis sur le topic en question, en conclusion.
Je veux bien reprendre ça avec toi si besoin est, notamment la répartition des courants de Foucault en surface...

Bonsoir,

Corrigez moi si je me trompe mais il n'y a pas une histoire d'effet de peau et donc de courant relativement concentré à la surface.

Je vais vérifier de mon coté.

Amicalement,

Benjamin

A mon avis, non...
L'effet de peau apparaît avec un champ magnétique alternatif ou plus généralement variable.
Ici, le champ magnétique est continu (sauf sur les "bords"). On peut se poser la question si c'est la même chose avec un flux variable. Mais je n'y crois pas trop...

Bonsoir, merci pour le lien, Je l'ai bien regardé. Moi aussi j'ai commencé par construire une maquette pour réaliser une expérience mettant en évidence le freinage à courants de Foucault. Ma modélisation n'est pas vraiment la même: je fais passer une lame en aluminium (très fine) entre des aiments (qui créent un champ magnétique uniforme). J'observe bien un freinage de la lame et je vois donc l'effet de la force de Laplace (qui est ma force de freinage) proportionnelle à la vitesse de la lame. Mais comment l'écrire? J'ai lu qu'il existe une formule théorique mais qu'en général il est normal de retrouver avec cette formule les calculs théoriques mais à un facteur près, ce serait à cause de la répartition en surface des courants...Pourriez-vous m'aider?

Comment se déplace la lame d'aluminium ?
On peut imaginer un pendule avec la lame d'aluminium comme masse...
Comment fais-tu pour déplacer la lame d'aluminium ?

Bonsoir
Pour moi, il n'y a pas du tout de mouvement de rotation. Le mouvement est rectiligne. J'ai fixé la lame sur un mobile qui se déplace en suivant un plan incliné. J'ai fixé les aimants sur un portique. Je lâche le mobile et la lame passe entre les aimants. J'observe bien un ralentissement du mobile dès que la lame est plongée dans le champ magnétique, c'est à dire sous le portique.

OK, je vais faire le calcul pour voir ce que ça donne...

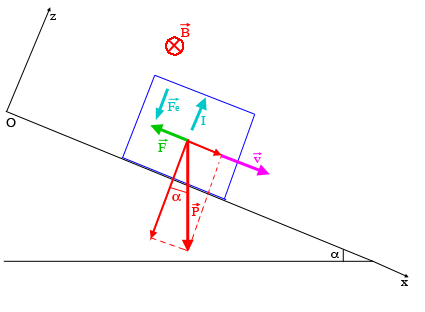
On prend le repère le plus pratique, à savoir l'axe x selon le plan incliné, l'axe z perpendiculaire au plan incliné et vers le haut, l'axe y étant orienté vers l'arrière pour faire un trièdre direct avec les deux autres.
Le champ magnétique est orienté vers l'arrière (selon Oy).
Comme il est question de courant (surfacique notamment), j'ai fait le calcul avec le courant.
On a :

Le champ est le champ électromoteur  

D'autre part, on a :


S étant l'aire de la section de la plaque (perpendiculaire à l'axe z). Pour la partie plongée dans le champ magnétique, on peut dire que la partie de la plaque a une longueur l suivant x et une épaisseur suivant l'axe y ==> S = l .


La force de Laplace est donnée par :



Si on appelle L la longueur de la partie de la plaque, suivant l'axe z, qui est plongée dans le champ magnétique :

Donc :


  est d'ailleurs le volume de la partie de la plaque plongée dans le champ magnétique.
Passons à la partie "mécanique"...

En projetant sur l'axe x :




Je ne détaille pas la résolution de l'équation différentielle (sauf demande).
En posant  

   étant la vitesse initiale à l'entrée dans la zone du champ magnétique.
A comparer à la vitesse sans champ magnétique au même endroit :  

Remarques :
1) Ce calcul peut contenir d'éventuelles erreurs
2) Ce calcul ne constitue qu'une première approche sans doute
3) Le champ magnétique a une forme "rectangulaire" selon l'axe x. Il est bien évident que le champ magnétique ne commence pas et ne s'arrête pas brusquement. Il faudrait voir s'il n'est pas possible de faire une modélisation plus fine, en forme de trapèze par exemple (décroissance linéaire du champ).
4) Ce calcul ne tient pas compte de l'entrée et de la sortie de la plaque dans le champ magnétique. A l'entrée comme à la sortie, il n'y a qu'une partie de la plaque qui est plongée dans le champ magnétique donc la force n'est pas la même.  

Bonsoir
Merci beaucoup pour l'aide. Je vais étudier tout cela.

bonsoir,

je travaille sur le freinage d'un "véhicule" (deplacement d'une fusée a vapeur sur un rail), et en cherchant des solutions sur le freinage magnétique je suis tombée sur ce topic. J'ai un probleme pour calculer la vitesse de mon mobile a partir du debut du freinage.

pour cela, j'ai utilisé le theoreme m*a = F+L, ou F est la poussee de ma fusee (consideree constante et toujours presente pendant le freinage) et L la force de laplace obtenue grace aux aimants.

apres calculs, je trouve v(t) = (v0 - F/Mk) * exp(-kt) + F/Mk
                         d(t) = -1/k * (v0 - F/Mk) * (exp(-kt) -1) + F/Mk * t
les appellations sont les memes qu'au dessus, avec F la poussee, M la masse de mon mobile (supposee constante) et v0 la vitesse en debut de freinage.
mon raisonnement est il juste?
j'aimerai maintenant m'affranchir du temps pour reussir a faire un graphe de v selon d.

merci pour votre aide

OK, je regarde ça...

merci!

dans le pire des cas, il suffit simplement que je fasse une courbe parametree sur matlab avec d en abscisse et v en ordonnée!
mon souci est plus dans l'exactitude de mes reponses..

Il y a une erreur dans le calcul de v(t) parce que :
1) F/Mk n'est pas homogène à une vitesse
2) j'ai fait le calcul et je trouve F/k à la place de F/Mk
(F/k est bien homogène à une vitesse)

De plus, ce n'est pas e^-kt parce que  kt  devrait être sans dimension, ce qui n'est pas le cas...
C'est e^-(k/m)t.
(m/k a bien la dimension d'un temps).

pourtant k=sigma*L*l*delta*B²/M,
en dimension:
sigma=I² T^3 L^(-3) M^(-1)
L*l*delta = L^3
B² = (M T^(-2) I^(-1))²

ce qui donne I2 T3 L(-3) M(-1) L3 M2 T(-4) I(-2) M(-1) = T(-1)

pour moi c'est homogene a "l'inverse du temps"

je pense qu'il manquait la division par la masse dans l'expression de k... non?

OK, je n'ai pas pris le même "k" dans le calcul que je viens de faire...
Donc je retire ce que j'ai dit.
On peut exprimer d en fonction de v mais v en fonction de d, c'est nettement plus difficile (voire impossible analytiquement)

d'accord
mais avec matlab j'ai réussi à faire des courbes paramétrées, et n'ayant pas absolument besoin de l'expression analytique, ça ira!
merci beaucoup d'avoir vérifié mes calculs, et peut-etre a bientot si j'ai d'autres questions...

OK

Pour en revenir a la question initiale, il faut definir la zone superficielle. Or cela s'entend par rapport a l'epaisseur d'un volume. La plus faible que l'on puisse ecrire est celle d'une epaisseur atomique (3-5 A). Quelque soit les materiaux on est loin de ca avec les courants de Foucault, mais quand meme on peut faire des choses avec la frequence et les conductivites des substrats.
Il vaut mieux s'interesser a la detection des defauts qui peuvent etre de surface et la bien detecté même si leur epaisseur est fine. On peut également avec des sondes analyser l'interieur des tubes et voir des defauts soit sur la surface interne du tube soit sur la surface externe. Tout ca est loin du freinage mais bien mieux adapté au theme TIPE de cette année.

Quel jour la presentation du TIPE a Paris?