Personne pour m'aider svp?

Bonjour,
Pas très simple comme problème...
Effectivement, le disque est "ouvert". D'où vient donc le courant ?
Lorsque le disque tourne, les électrons vont à la même vitesse que le disque (on peut considérer que la vitesse des électrons est nulle par rapport au disque). Plus on est éloigné du centre, plus la vitesse linéaire est élevée (v = R).
Les électrons sont soumis à la force de Lorentz  . Donc il se crée un courant radial dont le sens dépend du sens de l'induction magnétique et du sens de rotation.
Ce courant avec l'induction magnétique va créer une force    qui va s'opposer à la rotation.
Plus la vitesse est grande, plus la force est grande (donc totalement inefficace au repos).
Plus l'induction magnétique est grande, plus la force est grande.
Avec un schéma, c'est plus clair... Je vais essayer d'en faire un...

Bonjour,
Merci pour votre réponse je vois déjà beaucoup mieux, j'ai calculé la force de Lorentz auxquels les électrons sont soumis, elle est bien radiale et négative (par rapport à mon schéma). Par contre, pour la force de Laplace, à quoi va correspondre le dl ? est-ce le contour extérieur du disque où est-ce juste la partie du disque plongée dans le champ, (c'est à dire un demi disque dans ma modélisation).
Je vais essayer de poster moi aussi un schéma.

Merci beaucoup pour la réponse,
Xavier

Voilà le schéma :

Dans ce cas, les électrons sont soumis à une force qui les déplacent vers l'intérieur du disque. Le sens conventionnel du courant est donc du centre vers la circonférence selon les rayons.
dl, c'est un morceau infinitésimal du rayon. Si le champ magnétique peut être considéré comme constant, on n'a pas besoin de faire une intégration. Si le champ est constant sur tout le rayon, on a I R B en norme et comme direction, opposé à la rotation (dirigé vers la droite pour le rayon selon Oy).
Tout cela se règle avec des produits vectoriels et je ne sais pas si tu es très familiarisé avec...
Un TIPE, c'est en 1ère, non ?

Non, en première c'est le TPE, le TIPE c'est en prépas, en SUP et en SPE. Moi en l'occurrence je suis en SPE et l'électromagnétisme était au programme. Donc concernant les produits vectoriels, je suis bien familiarisé avec!
Par contre est-ce que vous pouvez me détailler un peu plus le calcul pour la force de Laplace car je n'arrive toujours à avoir un résultat cohérent.
Merci beaucoup,
Xavier

Ouf ! Cela me paraissait un peu "balaise" pour la 1ère...
Je te réponds un peu plus tard. J'ai quelque chose d'urgent à faire...

En attendant, un schéma...

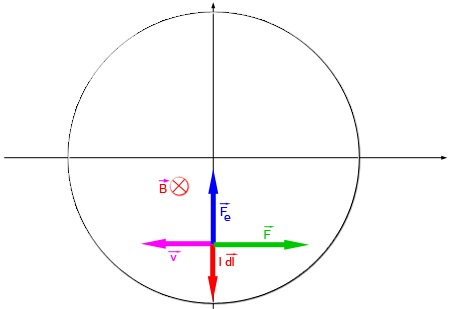
v est la vitesse linéaire ou tangentielle
B est l'induction magnétique
F_e est la force exercée sur les électrons
F est la force de freinage

On peut aussi dire que    (loi d'Ohm locale).
Ici, il n'y a pas de champ électrique créé par une tension. C'est le champ électromoteur  
Donc  

C'est simplement une autre façon de le dire. A mon avis, en voyant l'action de la force de Lorentz sur les électrons, on voit mieux comment se crée le courant mais...

c'est sur que le pauvre première qui se serait mis là dedans, je le plains!

pour la force électromotrice et la densité de courant, ce sont bien les calculs que j'avais fais...ouf! Par contre pour pour le I.dl, ça va correspondre à I.(-dr) sur mon schéma et donc je l'intègre entre O et R (rayon du disque) ?
Par contre si je poursuis le calcul j'aurais ma force qui dépendra seulement de I, R et B, mais pas de la vitesse, ce qui n'est pas normal, si?
Car selon mon expérience et toutes les explications que j'ai pu lire à droite et à gauche, l'efficacité du frein dépend de la vitesse et de la puissance du champ...
En revanche pour la force de Lorentz, j'ai bien une expression en fonction de B, , et R.

Merci beaucoup du temps que vous m'accordez,
Xavier

Je suis allé un peu plus loin...
En fait, le courant n'est pas constant sur un rayon parce qu'il dépend de la vitesse. Or, un point situé loin de l'axe va plus vite qu'un point situé près de l'axe.
De plus, je pense que ce qui compte, c'est le moment de la force : c'est un couple résistant.
Je vérifie à nouveau mes calculs ...
Pour le I.(-dr), je ne suis pas très d'accord parce que le courant est orienté vers l'extérieur du disque donc dans le sens de l'axe r. Donc je mettrais plutôt I.dr...
Et il faut intégrer mais sur le moment, pas sur la force, je pense...

"ma force qui dépendra seulement de I, R et B, mais pas de la vitesse, ce qui n'est pas normal, "==> Elle va dépendre de la vitesse parce que I n'est pas constant. En fait, il faut considérer un anneau de rayon r et r+dr sur le demi-cercle (si on considère que tout le demi-cercle est dans un champ magnétique constant). Le courant est le même en tous les points de cet anneau.

J'ai vérifié mes calculs mais je ne suis pas entièrement satisfait...
On considère le cas d'un disque de rayon a qui tourne dans le sens trigonométrique positif (donc pas comme sur le schéma que j'ai fait). dans l'autre sens, il y a une histoire de signe qui me gêne (que j'ai solutionnée par la suite).
Sur un rayon, on a le champ électromoteur :




Tous les rayons soumis au champ magnétique fournissent cette fem et tous ces générateurs élémentaires sont en parallèle.
Si R est la résistance du circuit (résistance du disque) :

Dans ce cas (tout est inversé par rapport au schéma sauf l'induction magnétique), le courant va de l'extérieur vers l'intérieur du disque donc   .
On a donc :




Le moment de cette force par rapport à l'axe est :





D'où :



  avec  

Je ne suis pas entièrement satisfait. J'aimerais trouvé un résultat qui ne dépende pas de R, résistance du disque qu'on ne connaît pas puisqu'on ne sait pas quel est le chemin parcouru par le courant dans le disque.
Mais je suis un peu gêné par la densité de courant qui n'est pas la même sur un rayon puisque v est différente selon la position du point...
Je préfèrerais trouver un résultat en fonction de plutôt que de R.

je suis désolé mais je poense qu'il y a une erreur : lorsque tu calcul e, je suppose que c'est le flux magnétique. Si c'est bien ca, alors il y aurait une erreur de signe, car d(PHI)=-Em dt avec Phi, le flux ...

non,c'est parfait et j'ai rien dit. parcontre,peu être peux tu trouver une relation entre R et p en concidérant que le conducteur est cyllindrique de rayon r, de longueur l.

on aurait ainsi R = p L/(Pi*r²)

OK... Mais il faut considérer que le courant est radial et que ça se passe seulement dans le demi-disque inférieur. A mon avis, il faut prendre des secteurs circulaires d'angle d et intégrer de 0 à ou quelque chose qui ressemble...

soit l l'épaisseur du cylindre et a le rayon.

=*E
i =*dS
i=*2**a*l

d'où E=i/(2**a*l*)


d'autre part, E=-grad(V)
-dV=E*dl
V1-V2=U=E*dl
U=i/(2**l*)

on sait que U=Ri

on en déduit que R=/(2l)

Il faut que je réfléchisse mais, a priori, je ne suis pas vraiment d'accord avec ce calcul parce que  2 a l  représente la surface latérale du disque. Or il y a des courants induits dans tout le demi-disque inférieur et pas seulement sur le bord du disque.