Inscription / Connexion Nouveau Sujet
Thevenin Norton
Bonjour,
Je reviens vers vous car il y a quelques exos d'électricité que je ne comprends pas même en ayant les résultats...
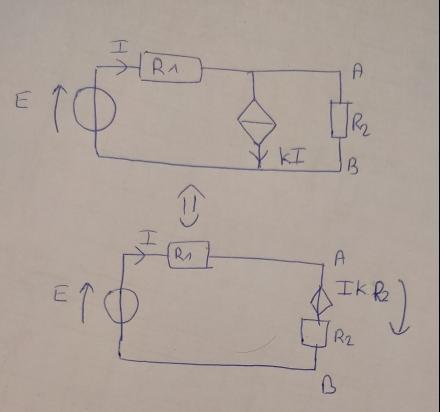
Dans cette exo, je dois calculer le générateur de Thevenin (Rth et Eth)
Cependant les sources sont liées (je ne sais plus ce qu'est la différence sur le schéma entre liée et non)
J'ai donc fait un schéma équivalent, mais je ne sais pas si il est bon, car je ne retrouve pas la correction
Merci !
Bonjour
Pour Eth :
méthode habituelle.
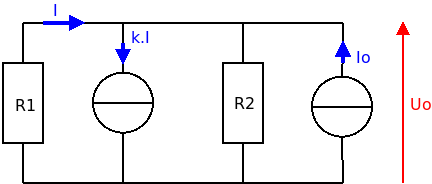
Pour Rth, tu éteins la source indépendante en conservant la source lié. Tu branches un générateur idéal de courant Io. La tension obtenue est
Rth.Io.
Je suis désolé mais je n'arrive pas à mettre en équations à cause de IKR2 (la tension de la source liée)
Sans celle ci j'aurais fait Eth = E.R2 / ( R1+ R2) et Rth = R1.R2 / (R1 + R2 )
Avec les sources liées il faut se méfier des transformations Thevenin Norton. La loi des noeuds et la loi des mailles conduisent facilement au résultat.
Merci,
J'ai donc bien retrouvé Eth (tension sur R2) Eth= (E R2 (1-K) ) / ( R1 + R2 (1-K)), cependant je bloque sur les équations pour Rth:
J'ai
Io = -I + K*I + IR2 = -I(1-K) + V/R2
Rth Io = - I*R1
J'ai donc V en trop ici (tension sur R2)
Pour Eth : je crois que tu as compris l'essentiel mais attention si tu veux utiliser le schéma équivalent : Eth est la tension aux bornes de R2, pas celle aux bornes de l'ensemble formé de R2 en série avec le générateur de tension de fém k.R2.I
Pour Rth : Uo=Rth.Io
La loi des nœuds permet d'exprimer l'intensité du courant à travers R2 en fonction de Io, I et k. On élimine ensuite I en écrivant que les tensions aux bornes de R1 et de R2 sont égales.
Pour Eth : malgré ton schéma équivalent qui est faux comme expliqué précédemment, l'expression obtenue est correcte...
Bonsoir (dsl d'avoir pris si longtemps)
J'ai donc trouvé IR2 = Io + I(1-k)
J'ai fait Rth = Uo/Io
Avec Uo = IR2* R2 = R1 I
Donc Rth = R1 R2 / ( R2 (1-K) + R1)
Pour Eth j'ai utilisé le schéma de base car l'autre était faux
I = KI + IR2
E - R1 I - R2 IR2
V = R2 I2 = E - R1 I
V = E - R1 V / (R2(1-k))
Donc V = E R2 (1-k ) / (R2 (1-K) + R1)



