Inscription / Connexion Nouveau Sujet
Thermodynamique et le mercure.
Exo 1
Une masse m de mercure est placée dans un récipient de volume variable V initialement vide et placé dans un thermostat à T1=573K .
Le mercure liquide est incompressible et de volume massique vl= 7.7 10^(-5) m^3 /kg
Le mercure gazeux a
-pour volume massique à T1 V(v1)=0.700 m3 /kg
-pour pression de vapeur saturante P*(T1)=0.330 bar
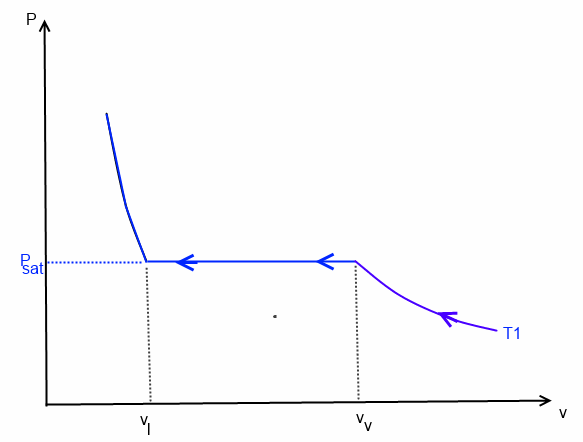
a- on comprime lentement le mercure à partir d'un grand volume .Décrire dans un diagramme de Clapeyron (P,v=V/m) l'évolution du système
b-la vapeur est elle sèche ou saturante pour Vo=8.00 m3 ; V1=1.00 m3 ?
Quelle est la valeur du titre x en vapeur dans chaque cas: xo,x1?
Un résistor chauffant à T3= 800K amène la masse m=8.0 kg de mercure primitivement à T1=573 K dans un volume V=1,0 m3 fixé à la température T2=673K
A cette température le mercure gazeux a:
-pour volume massique v (v2)=0.128 m3 kg-1
-pour pression de vapeur saturante P*(T2)=2.10 bar
a-Représenter la transformation réalisée dans le diagramme de Clapeyron
b-Calculer le titre final en vapeur x2 et la variation de la quantité liquide entre l'état initial et l'état final
c- calculer l'énergie thermique reçue par le mercure.
d-calculer la variation d'entropie du mercure puis faire un bilan entropique: entropie d'échange,entropie de création
Alors déjà dans cet exercice je n'ai pour l'instant rien fait car y-aurait-il quelqu'un qui pourrait commencer par m'aider pour la toute première question car je ne sais pas trop comment commencer..
Merci à vous d'avance !
bonjour,
1a) tu dessines un diagramme Pv, l'isotherme T1 et puis tu représentes une transformation en partant d'un point où V est "grand" (corps totalement gazeux)
1b) il faut la masse m pour répondre
Je dois quitter, je reviens dans 1h15 à peu près et je vous dit si j'ai réussi à avancer !
Cependant, j'ai du mal à tracer les diagrammes (P,v) sauriez-vous m'indiquer une technique car j'ai du mal avec les abscisses à bien les utiliser je ne sais pas si vous voyez..
Merci d'avance !
Comment fait-on pour mettre une photo sur le site pour vous montrer le diagramme que j'ai fait..
Cependant je n'ai pas mit la cloche car je ne cerne pas très bien à quoi elle sert ?
1b) Vous avez dit
il faut la masse m pour répondre
J'ai trouvé mais l'image est trop grosse..
En gros j'ai dessiné l'isotherme T1 avec une branche quasi-verticale à droite (zone du mercure liquide), la branche horizontale qui correspond à P* = 0,330 bar (zone du mélange liquide/vapeur) et à gauche, une branche qui décroit (zone de la vapeur uniquement). Les extrémités de la branche horizontale sont le point L à gauche d'abcisse vl = 7,7*10-5 m3/kg et le point V à droite d'abscisse vv = 0,700 m3/kg est-ce que vous voyez à peu près ?
Oui c'est exactement ça !  .
.
Cependant je n'ai pas mit la cloche car je ne cerne pas très bien à quoi elle sert ?
Pour la question b) j'ai fait ça:
- v0 = V0/mt = 8,00/8,0 = 1 m3/kg ce qui correspond à de la vapeur sèche.
- v1 = V1/mt = 1,00/8,0 = 0,125 m3/kg ce qui correspond à de la vapeur saturante.
Est-on d'accord pour ça ?
Après en cas général on xv = (vt-vl)/(vv-vl).
- x0 = (v0-vl)/(vv-vl) = (1-7,7*10-5)/(0,700-,7*10-5) = 1,42 ce qui représenterais 142% donc j'ai un problème mais où ?
- x1 = (v1-vl)/(vv-vl) = (0,125-7,7*10-5)/(0,700-,7*10-5) = 0,17 ce que représenterais 17% ça me parait possible..
Qu'en pensez-vous ?
la "cloche" est appelée la courbe de saturation et elle indique la variation de vl et de vv en fct de T
c'est une caractéristique du corps étudié
mais ici on ne peut pas la tracer, on n'a pas assez d'infos
D'accord merci pour l'information .
.
J'ai posté un message juste avant, je ne sais pas si vous l'avez vu car peut être qu'on a posté en même temps..
la formule n'a de sens que si v est compris entre vl et vv
en dehors de ces deux valeurs on n'a plus affaire à un mélange diphasique
par ex. si v > vv alors xv = 1 (le corps est en phase gazeuse uniquement)
D'accord donc c'est pour ça que j'ai un problème pour x0 qui est en réalité égal à 1 et x1 = 17% vous semble-t-il raisonnable ?
J'ai commencé la 2ème partie:
a) J'ai réalisé le même type de graphique qu'à la 1ère partie sauf qu'en abscisses on a pas les mêmes valeur et on ne connait vl cette fois..
b) Du coup, du fait qu'on ne connaisse pas vl, je ne sais pas comment faire pour déterminer x2..
Est-ce que du fait que dans l'énoncé ils disent que Le mercure liquide est incompressible et de volume massique vl= 7.7 10-5 m3/kg on garde le même vl que pour la 1ère partie ?
Comment ça ce fait ? C'est du fait que le mercure est incompressible à l'état liquide ?
Je trouve donc xv = 97%.
Par contre pour calculer la variation de la quantité liquide entre l'état initial et final je ne sais pas trop si c'est la bonne méthode:
x1 c'est l'état initial et l'état final c'est x2 ?
Pour l'état initial on a donc xl = 1 - x1 = 0,83.
POur l'état final on a donc xl = 1 - x2 = 0,03
or xl = ml/mt donc:
ml,i = xl,i*mt = 0,87*8 = 6,96 kg.
ml,f = xl,f*mt = 0,03*8 = 0,24 kg.
Donc Δml = ml,f - ml,i = 0,24 - 6,96 = 6,72 kg.
Qu'en pensez-vous ?
vl est constant donc en diagramme Pv c' est une droite verticale (v=vl)
(incompressible => la masse volumique est indépendante de la pression)
D'accord c'est comprit pour la droite verticale c'est logique du coup  .
.
Avez-vous vu ce que j'ai proposé sur mon post ?
vl étant très petit je trouve :
x1  0.125/0.7 = 17.9%
0.125/0.7 = 17.9%
x2  0.125/0.128 = 97.7%
0.125/0.128 = 97.7%
et  ml = -0.798 x8 = -6.4 kg
ml = -0.798 x8 = -6.4 kg
Oui c'est aussi ce que je trouve, j'avais fait des arrondi  .
.
Pour la suite,
c- calculer l'énergie thermique reçue par le mercure.
J'ai dit ceci pour le moment:
1er principe de la thermo': ΔU = W+ Q or ici V=cste donc ΔU = Q.
Je suis tombé sur le corrigé sur internet où il calcul ΔU en 3 étapes mais je ne veux pas recopier et j'aimerais que vous m'expliquiez comment s'y prendre car je ne comprend pas trop.. Si ça se trouve vous avez une autre technique ?
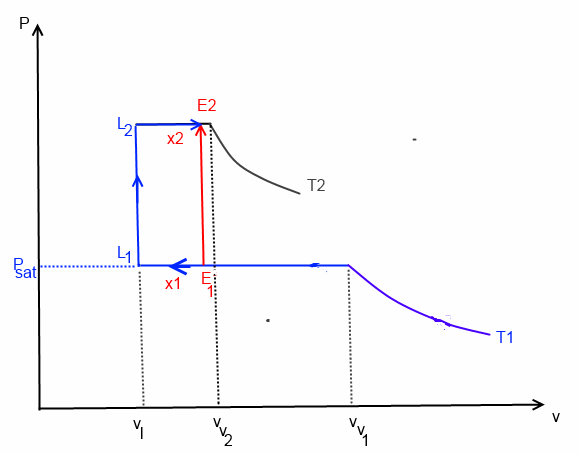
j'ai essayé de représenter la situation sur le dessin qui suit:
(E1,E2) est la transformation à étudier (en rouge).
c'est une isochore donc Q =  U
U
comme U est une fonction d'état, sa variation ne dépend pas du chemin suivi donc on peut faire le calcul sur le chemin qu'on veut liant E1 et E2
le chemin bleu (E1,L1,L2,E2) doit te permettre de faire le calcul
c'est pour cela que tu dois avoir trois étapes
Oui c'est bien cela je pense et j'ai comprit avec votre explication, je me suis lancé dans la première étape:
E1-->L1:
ΔH = ΔU + Δ(PV) = W + Q + Δ(PV).
W = -∫VfVi PdV = -P*(T1)*ΔV mais que vaut ΔV ici je n'arrive pas trop à voir ? :/.
Oui c'est bien cela je pense et j'ai comprit avec votre explication, je me suis lancé dans la première étape:
E1-->L1:
ΔH = ΔU + Δ(PV) = W + Q + Δ(PV).
W = -∫ViVf PdV = -P*(T1)ΔV mais que vaut ΔV ici je n'arrive pas trop à voir ? :/.
Pareil pour Δ(PV) on aura Δ(PV) = P*(T1)ΔV mais que vaut ΔV aussi..
(E1,L1) est la liquéfaction d'une masse m x1 de vapeur à T=T1=cste et P1=Psat(T1)=cste
donc  U1 = W+Q = m x1 Lliquéfaction - P1
U1 = W+Q = m x1 Lliquéfaction - P1  V
V
avec V = mv
donc ici  V = mvl - m x1 v1
V = mvl - m x1 v1
sauf erreur
Ce que je ne comprends pas c'est: ΔV = mx1vl - m x1 v1.
Car vous avez dit en (E1,L1) est la liquéfaction d'une masse m*x1 de vapeur à T=T1=cste et P1=Psat(T1)=cste mais ce ne serait pas plutôt la liquéfaction d'une masse m*xv de vapeur ?
De plus pour ΔV = Vf-Vi.
Si j'essaye de déterminer Vf et Vi séparément pour mieux comprendre:
- Vf = VL1 = masse de liquide en L1 * le volume massique de liquide en L1 = ml*vl2 = xl*mt*vl2 non ?
- Vi = VE1 = masse de ???? C'est ça que je ne comprend pas, on met quoi car en E1 on a du liquide et du gaz ?
Merci d'avance !
en thermo il faut bien définir le système qu'on étudie
en E1 on a une masse m x1 de vapeur et m(1- x1) de liquide (on n'a donc pas uniquement de la vapeur)
en L1 on a une masse m de liquide seul; donc la transformation est la liquéfaction d'une masse m x1 de vapeur (le liquide déjà présent en E1 ne se transforme pas, seule la vapeur présente en E1 subit une transformation et le système considéré ici est cette vapeur)
D'accord donc si ej reprend et si j'essaye de déterminer Vf et Vi séparément pour mieux comprendre:
- Vf = VL1 = masse de liquide en L1 * le volume massique de liquide en L1 = ml*vl = mt*vl car en L1 si tout s'est transformé en liquide, ml = mt non ?
- Vi = VE1 = masse de ?? Je bloque toujours, je sais que on a m*x1 de vapeur et m(1- x1) de liquide mais comment écrire Vi ?
si tu prends comme système la masse m de Hg
en L1: Vf = m vl
en E1: Vi = m x1 v1 + m(1-x1) vl
et en calculant Vf-Vi tu trouves la même chose que moi
D'accord pour Vf, ça pas de soucis.
Pour Vi j'avais trouvé seul, Vi = ml*vl + mv*vv = xl*m*vl + x1*m*vv mais après vous, vous passez à = xl*m*vl + x1*m*v1 donc, vv en E1 = v1 mais pourquoi ???
Car v1 c'est le volume massique totale (liquide+vapeur) non ? donc différent de vv qui est juste le volume massique de vapeur non ?
oui, effectivement, attention aux notations;
ce que j'ai noté v1 c'est en fait vv1 (cf dessin ci-dessus)
Ha oui d'accord !
Donc si je résume, j'ai:
E1 --> L1:
ΔU1 = m*l(T1) - P*(T1)[mx1vl-mx1vv1].
L1 --> L2:
ΔU2 = mcl(T2-T1).
L2 --> E2:
Par la même méthode que pour E1 --> L1 j'ai:
ΔU3 = ml(T2) - P*(T2)[mx2vv2-mx2vl].
Donc ΔU = ΔU1 + ΔU2 +ΔU3 = m*l(T1) - P*(T1)[mx1vl-mx1vv1] + mcl(T2-T1) + ml(T2) - P*(T2)[mx2vv2-mx2vl] est-on d'accord pour ça ?
Je trouve ΔU = Q = 4866364 J mais ça me paraît bizarre..
J'ai prit ça comme valeur:
m = 8kg.
l(T1) = 297,0*10³ J/kg.
l(T2) = 293,7*10³ J/kg.
T1 = 573 K.
T2 = 673 K.
vl= 7.7 10-5 m³/kg
vv1 = 0.700 m³/kg
P*(T1)= 0.330 bar = 0,330*10⁵ Pa.
P*(T2) = 2,10 bar = 2,10*10⁵ Pa.
vv2 = 0.128 m³/kg.
Me serais-je trompé dans les unités ?
attention, (E1 L1) est une liquéfaction donc Q1<0, Q1 = - m x1 Lvap(T1)
(L2,E2) est une vaporisation donc: Q2 = + m x2 Lvap(T2)
Oui en plus je l'ai noté !
Mais moi j'ai:
- Pour (E1 L1): Qp = ml*lliquéfaction(T1) = -ml*l(T1) = m*xl*l(T1) = m*(1-x1)*l(T1) non ?
- Pour (L2,E2): De même Qp = ml*lvaporisation(T2) = m*xl*l(T2) = m*(1-x2)*l(T2) non ?
Rectification:
- Pour (E1 L1): Qp = ml*lliquéfaction(T1) = -ml*l(T1) = m*xl*l(T1) = m*(1-x1)*l(T1) non ?
- Pour (L2,E2): De même Qp = mv*lvaporisation(T2) = m*x2*l(T2) non ?
Encore une rectification:
- Pour (E1 L1): Qp = ml*lliquéfaction(T1) = -ml*l(T1) = -m*xl*l(T1) = -m*(1-x1)*l(T1) non ?
- Pour (L2,E2): De même Qp = mv*lvaporisation(T2) = m*x2*l(T2) non ?
ΔU = ΔU1 + ΔU2 +ΔU3 = -m*x1*l(T1) - P*(T1)[mx1vl-mx1vv1] + mcl(T2-T1) + ml(T2) - P*(T2)[mx2vv2-mx2vl] est-on d'accord pour ça ?
Et avec les valeurs de toutes à l'heure, je trouve ΔU = 2013396 J..
Je me suis trompé à la calculette je trouve au final ΔU = 1803554 J = 1804kJ est-ce un bon arrondi ?
Je fais la dernière question 
Pour la question d) je bloque à un truc:
J'utilise la 1ère identité thermo': dU = -PdV + TdS.
Pour la chemin E1-->L1 et L2-->E2, T = cste et V = cste donc dU = TdS d'où ΔU = TΔS et donc:
- ΔS1 = ΔU1/T1.
- ΔS2 = ΔU2/T2.
Mais c'est ΔS3 que j'ai du mal car quand on passe de L1-->L2 la température varie donc on a ΔU = Δ(TS) mais comment faire ?
en négligeant vl je trouve:
Q  m [ x1(p1vv1 - Lvap1) + x2(Lvap2 -P2vv2) + cl(T2-T1) ]
m [ x1(p1vv1 - Lvap1) + x2(Lvap2 -P2vv2) + cl(T2-T1) ]
il me manque c Hg liq
Pour le chemin E1-->L1 et L2-->E2, T = cste et V = cste
non, le volume varie, c'est la pression qui est cste donc il faut utiliser dH = ...
pour (L1,L2) si on suppose le liquide incompressible alors on a:
dU = m cl dT
et dU = TdS donc dS = ...
et on trouve
 S en intégrant
S en intégrantOui cl = 0,135 kJ/kg/K.
Je reviens sur ce que vous avez dit pour le chemin E1-->L1 et L2-->E2, on T = cste et V est bien constant car on est dans le cas ou V est fixée ) 1,0m³ au début de la deuxième partie c'est marqué..
C'est bon j'ai rectifié:
- ΔS1 = ΔH1/T1.
- ΔS3 = ΔH3/T2.
- ΔS2 = m*cl*ln(T2/T1).
Je trouve ΔS = 2,846 kJ/K.
Mais comment s'y prendre pour déterminer séparément Sc et Se ?
J'ai dit que Se = ∫(δQ/Text) = ∫(δQ/T3) = Q/T3.
Sauf que dans la correction qu'il donne sur internet que j'avais trouvé, ils disent que c'est Se = -Q/T3 mais d'où vient ce - ?