Inscription / Connexion Nouveau Sujet
Thermodynamique
Bonjour ,
Svp je bloque sur cet exercice
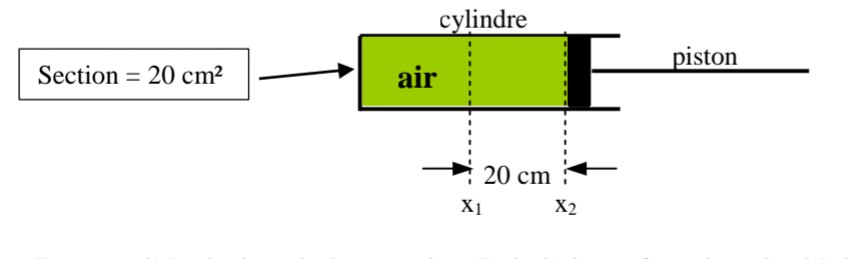
On comprime de l'air dans une chambre à air d'un vélo à l'aide d'une pompe . l'ensemble Pompe +chambre à air est modélisé par l'ensemble cylindre+piston ci-dessous :
1)Donnez l'évolution de la Pression P de l'air en fonction du déplacement x du piston.
2) Donnez l'évolution de la Pression P de l'air en fonction du volume V d'air dans le cylindre .
Je connais l'expression du travail des forces de Pression  w=-PextdV . Juste ça . Besoin d'une piste qui m'aidera.
w=-PextdV . Juste ça . Besoin d'une piste qui m'aidera.
Merci d'avance
Bonjour
deux cas sont envisageables : le corps de pompe est suffisamment bon conducteur et la transformation est suffisamment lente pour être isotherme. Les choses sont alors simples.
On peut aussi envisager une transformation rapide et donc adiabatique mais cela ne semble pas être le cas ici.
Transformation isotherme j'ai envisagé ça aussi . Compression isotherme d'un gaz parfait donc Text=Tgaz=T0 et Pext=Pgaz
on aura donc à une température T0 , PV=nRT0=cste , de plus
 w=-PextdV=-PgazdV=-nRTO
w=-PextdV=-PgazdV=-nRTO , or PV=cste donc d(PV)=0 c'est-à-dire que PdV+VdP=0 et donc
; à la fin je trouve l'expression du travail en fonction de la pression ou de la pression en fonction du travail mais ça ne réponds à aucune des deux réponses . Merci de m'aider d'avantage Svp
Dans l'énoncé, tel que tu l'as recopié, il n'est pas question de travail. Il faut je pense retenir l'hypothèse d'une transformation isotherme donc : PV=constante.
La question est très mal posée :
1° : l'état initial du gaz n'est pas défini
2° la variable x n'est pas clairement définie. A quelle position correspond la situation x= 0?
L'idée générale consiste je pense à remarquer que, lorsque le piston se déplace de  x, le volume varie de
x, le volume varie de  V=S.
V=S. x au signe près.
x au signe près.
Difficile d'en dire plus sans un énoncé complet et cohérent...
L'énoncé que j'ai copié est le même que celui de l'original . que me proposez-vous comme solution ? pour résoudre au moins l'exercice ? et
1° je pense l'état initial du gaz est en X1 et final en X2
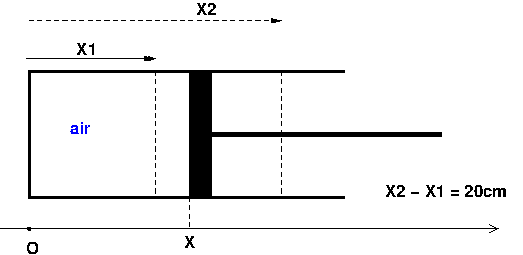
La question est d'exprimer P en fonction de x et cela n'est pas possible compte tenu des raisons écrites dans mon précédent messages. On peut évidemment remodeler l'énoncé pour le rendre précis conformément au schéma ci-dessous. x désigne la distance du "fond" du cylindre au piston. x1 et x2 sont les valeurs initiale et finale du piston, le piston se déplaçant ainsi vers la droite. Tu peux résoudre le problème dans ce cadre-là en guise d'entraînement.
Ok .
Pour cet énoncé :
1° Puisqu'on ne parle pas de travail dans cet exercice , l'unique réflexion qui me vient en tête est l'équation fondamentale de la statique des fluides :
dP= - airgdx ,
airgdx ,
Et ensuite on intègre de X1 à X2 ,
on a P(x2)-P(x1)= - airg(x2-x1) , je peux conclure que la pression suivant les x croissants .
airg(x2-x1) , je peux conclure que la pression suivant les x croissants .
Pour la question
2° on applique toujours l'équation :
dP=- airgdx or dV=S.dx ainsi on aura ,
airgdx or dV=S.dx ainsi on aura ,
dP=(- airg/s)dV
airg/s)dV
dP= , on trouve enfin :
P(x2)-P(x1) =
Réfléchis un peu aux ordres de grandeurs. L'axe du cylindre est horizontal et la pression est invariante, en statique, dans un même plan horizontal. Le diamètre du cylindre est d'environ 5cm. Entre le point haut et le point bas du gaz, la variation de pression est d'environ 0,6Pa alors que les pressions usuelles des gaz dans ce genre d'expérience sont de l'ordre de 105Pa. On peu donc considérer en excellente approximation la pression identique en tout point de l'air enfermé dans le cylindre. D'ailleurs, l'énoncé parle de la pression du gaz, sans préciser en quel point il faut la calculer.
Ici, les réponses sont hyper simples... Si on suppose T fixe, pour une même quantité de gaz on obtient :
P.V=P1.V1=P2.V2
avec la définition de x que j'ai fournie cela donne :
P.S.x=P1.S.x1=P2.S.x2 soit : P.x=P1.x1=P2.x2
Autre illogisme de ton énoncé : il faut logiquement répondre à la question 2 avant de répondre à la question 1.
Pour la conclusion de la 2° ,
V1< V2 ,
,
ln( et donc ,
P(x2)-P(x2) <0 donc la pression de l'air diminue quand le volume de celui-ci augmente .
Pour la conclusion de la 2° ,
V1< V2 ,
,
ln( et donc ,
P(x2)-P(x2) <0 donc la pression de l'air diminue quand le volume de celui-ci augmente .
Réfléchis un peu aux ordres de grandeurs. L'axe du cylindre est horizontal et la pression est invariante, en statique, dans un même plan horizontal. Le diamètre du cylindre est d'environ 5cm. Entre le point haut et le point bas du gaz, la variation de pression est d'environ 0,6Pa alors que les pressions usuelles des gaz dans ce genre d'expérience sont de l'ordre de 105Pa. On peu donc considérer en excellente approximation la pression identique en tout point de l'air enfermé dans le cylindre. D'ailleurs, l'énoncé parle de la pression du gaz, sans préciser en quel point il faut la calculer.
Ici, les réponses sont hyper simples... Si on suppose T fixe, pour une même quantité de gaz on obtient :
P.V=P1.V1=P2.V2
avec la définition de x que j'ai fournie cela donne :
P.S.x=P1.S.x1=P2.S.x2 soit : P.x=P1.x1=P2.x2
Autre illogisme de ton énoncé : il faut logiquement répondre à la question 2 avant de répondre à la question 1.

Mon raisonnement était quand même acceptable?
 Sinon pourquoi ?
Sinon pourquoi ?Mon raisonnement était quand même acceptable?
 Sinon pourquoi ?
Sinon pourquoi ?
Effectivement, quand x augmente de la valeur x1 à la valeur x2, la pression diminue de P1 à P2. J'ignore si l'énoncé demande de calculer le travail des forces de pression entre l'état 1 et l'état 2, cela en fonction de P1, S, x1 et x2.
Réfléchis un peu aux ordres de grandeurs. L'axe du cylindre est horizontal et la pression est invariante, en statique, dans un même plan horizontal. Le diamètre du cylindre est d'environ 5cm. Entre le point haut et le point bas du gaz, la variation de pression est d'environ 0,6Pa alors que les pressions usuelles des gaz dans ce genre d'expérience sont de l'ordre de 105Pa. On peu donc considérer en excellente approximation la pression identique en tout point de l'air enfermé dans le cylindre. D'ailleurs, l'énoncé parle de la pression du gaz, sans préciser en quel point il faut la calculer.
Ici, les réponses sont hyper simples... Si on suppose T fixe, pour une même quantité de gaz on obtient :
P.V=P1.V1=P2.V2
avec la définition de x que j'ai fournie cela donne :
P.S.x=P1.S.x1=P2.S.x2 soit : P.x=P1.x1=P2.x2
Autre illogisme de ton énoncé : il faut logiquement répondre à la question 2 avant de répondre à la question 1.
Effectivement, quand x augmente de la valeur x1 à la valeur x2, la pression diminue de P1 à P2. J'ignore si l'énoncé demande de calculer le travail des forces de pression entre l'état 1 et l'état 2, cela en fonction de P1, S, x1 et x2.


