Inscription / Connexion Nouveau Sujet
Thermodynamique
 etudiantilois
etudiantiloisBonjour,
J'ai des difficultés avec un exercice de thermodynamique.
On étudie le chauffage d'un bâtiment pendant une journée d'hiver. On suppose qu'à chaque instant tout le bâtiment est à la même température T. Soit C la capacité thermique du bâtiment. On suppose que le transfert thermique perdu par ce bâtiment à cause des fuites thermiques à travers les murs, le toit, etc... pendant la durée dt est :
 Qperdue=aC(T-Text)dt, a étant une constante positive.
Qperdue=aC(T-Text)dt, a étant une constante positive.
Application numérique : Text=263 K ; C=7,6*107 J.K-1 ; a=7,9*10-5 s-1.
a) On arrête le chauffage du bâtiment à la date t=0, la température étant T1=293 K. Etablir l'expression de la température T(t) ; donner l'allure de la courbe représentative de T(t). Calculer la température T du bâtiment au bout de trois heures.
b) On suppose maintenant qu'à t=0, la température est T0=275 K et le chauffage du bâtiment commence à fonctionner. Les radiateurs dégagent une puissance thermique P=210 kW constante. Calculer le temps t2 au bout duquel la température du bâtiment atteint la valeur T2=293 K. Au bout de combien de temps le régime permanent sera-t-il atteint si on maintient ce chauffage ?
Là où j'en suis :
Pour la question a, je pense utiliser le deuxième principe de la thermodynamique. Mais on ne sait pas si la transformation est réversible ? Je n'arrive pas à utiliser ce deuxième principe...
Merci par avance pour l'aide.
Bonjour
Pour la question a, je pense utiliser le deuxième principe de la thermodynamique
Le deuxième principe est un principe 'évolution qui permet de déterminer le sens spontané d'une évolution. Aucun intérêt pour cette première question puisque l'énoncé précise que le transfert thermique s'effectue spontanément l'hiver du bâtiment vers l'extérieur. En revanche, on peut utiliser le premier principe en supposant l'évolution isochore. Pour pouvoir considérer l'évolution réversible, il faudrait qu'à chaque instant, T soit égale, au premier ordre près, à Text ; ce n'est pas le cas.
dU=
 Q avec les conventions de signes usuelles. On peut poser à la date t :
Q avec les conventions de signes usuelles. On peut poser à la date t :
U=C.T (formule valide pour les solides et pour les gaz assimilables à des gaz parfaits.)
Bonjour,
Merci pour la réponse.
Donc ce qu'il faut utiliser c'est :  U = W+Q ?
U = W+Q ?
Et on a donc avec ce que vous avez écrit, en égalisant : W+Q=C.T.
Suis-je sur la bonne voie ?
Merci beaucoup.
Tu n'as pas lu attentivement tout ce que j'ai écrit : il faut appliquer le premier principe en supposant l'évolution isochore (travail nul) et, afin de pourvoir établir une équation différentielle, il faut l'appliquer à l'évolution élémentaire entre les instants de dates t et (t+dt). Comme déjà écrit :
dU= Q
Q
Tu es capable d'écrire la différentielle de U et attention au signe de  Q !
Q !
Tu devrais obtenir T solution d'une équation différentielle du premier ordre dont tu connais sûrement l'expression de la solution.
Merci pour la réponse.
Donc, comme le travail est nul, on a plutôt Q=C.T ?
Mais je ne sais pas où intervient ensuite dU= Q...
Q...
Je suis désolé, je crois que je ne comprends pas...
La question 1a est :
Établir l'expression de la température T(t)
Pour cela, il faut :
1 : établir l'équation différentielle vérifiée par T ; cela se fait en utilisant l'expression du premier principe entre les instants de dates t et (t+dt) comme expliqué dans mon message précédent.
2 : résoudre cette équation différentielle, ce qui va fournir l'expression T = f(t).
3 : répondre aux autres questions posées.
Bonsoir,
Voici ce que j'ai trouvé comme équation différentielle :
(dT/dt) = (P/C) - a(T - Text)
Est-ce que c'est juste ?
Merci beaucoup !
Et est-ce que la solution de cette équation différentielle est : t K
K exp(-at) + P/aC + Text. Avec C une constante réelle.
exp(-at) + P/aC + Text. Avec C une constante réelle.
Est-ce correct ?
Mais comment déterminer la constante C ?
Oui. Deux remarques tout de même :
1 : dans une première question, on demande d'étudier le cas particulier P=0.
2 : la constante K peut être déterminée à partir des conditions initiales.
Puisque tu as pris en compte dès le début la puissance de chauffage, tu as l'expression littérale de T. Reste à faire les applications numériques.
Le régime permanent est le cas limite tel que .
Bonjour srvo2021
Il y a je crois un minimum d'honnêteté intellectuelle à respecter sur un forum. Dans ton message du 02-10-19 à 21:04 tu écris :
Voici ce que j'ai trouvé comme équation différentielle :
(dT/dt) = (P/C) - a(T - Text)
Il s'agit en fait d'une formule qui t'a été fournie sur un autre forum le 01/10/2019 - 09h15 ...
* modération > autant donner le lien
Bonjour Vanoise,
C'est vrai, vous avez raison. Mais j'ai aussi essayé de mon côté de la trouver seule. Et c'est moi, seul, qui ai trouvé la solution.
Pour le régime permanent :
il n'y aurait pas une histoire de 5 tau ? C'est-à-dire que le régime permanent serait atteint au bout de t=5 tau ?
Mais ici que représenterait tau ?
Merci beaucoup.
a.t=(t/ ).
).
Tu peux vérifier en raisonnant sur les unités : (1/a) a bien la dimension d'un temps.
La question est mal posée : on ne peut pas trouver une valeur précise à l'obtention du régime permanent puisque le régime permanent correspond à une limite asymptotique. Cependant, l'habitude est de poser en physique exp(-x) 0 pour x
0 pour x 5.
5.
Merci pour la réponse.
Mais je n'ai donc pas compris : que faut-il donc répondre au sujet de ce régime permanent ?
Ce qui vient d'être dit : pour t (5/a), exp(-a.t)
(5/a), exp(-a.t) 0 ; la température est donc indépendante du temps : le régime permanent est atteint et correspond à une température égale à ...
0 ; la température est donc indépendante du temps : le régime permanent est atteint et correspond à une température égale à ...
Je te laisse faire le calcul...
Merci pour la réponse.
Je ne comprends pas : on nous demande le temps et pas la température du régime permanent ?
Et de toute façon on ne peut pas déterminer le temps car puisque l'exponentielle s'annule on n'a plus de "t" dans la solution de l'équation différentielle, non ??!
Il doit y avoir quelque chose qui m'échappe, mais je ne vois pas quoi...
Bonjour,
J'ai finalement trouvé :
question a : la température au bout de 3 heures est de 292,4 K. Est-ce cela ?
question b : t2=5h et 23 min.
t du régime permanent = 7 heures et 11 minutes.
Est-ce cela ?
Par contre, j'ai vraiment un problème pour tracer l'allure du graphe, j'ai essayé de le tracer sur ma calculatrice, et rien ne s'affiche !
Quelle est donc son allure et que placer d'intéressant sur la courbe ?
MERCI beaucoup ! (Il est beaucoup trop tard, je traîne trop sur cet exercice et j'ai cours tout à l'heure.....)
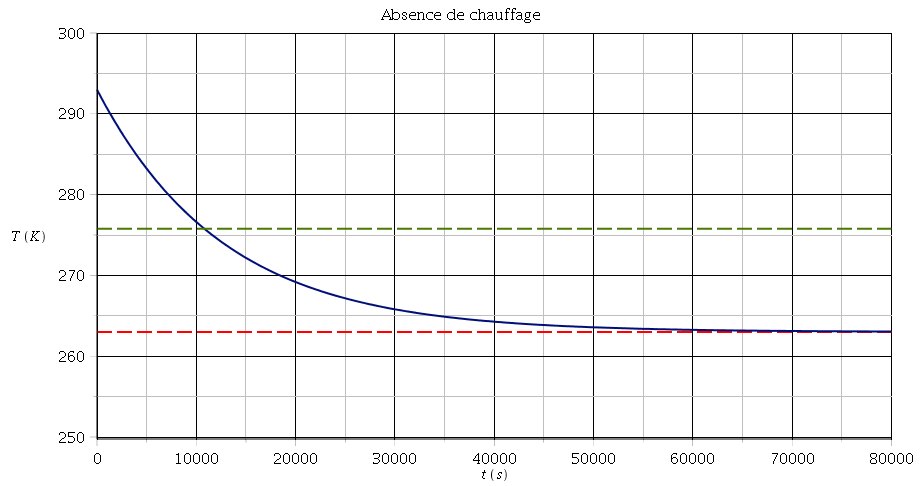
Pour la question a) : La baisse de température en 3h d'absence de chauffage est nettement plus importante que celle que tu obtiens (voir pointillé vert sur le graphe). Ton résultat n'est pas réaliste !
Pour l'allure de la courbe T=f(t) en absence de chauffage, tu peux repérer la température initiale T1, la température limite Text, la courbe étant sensiblement confondu avec l'asymptote pour t>(5/a). Cela donne l'allure ci-dessous, l'équation de la courbe étant :
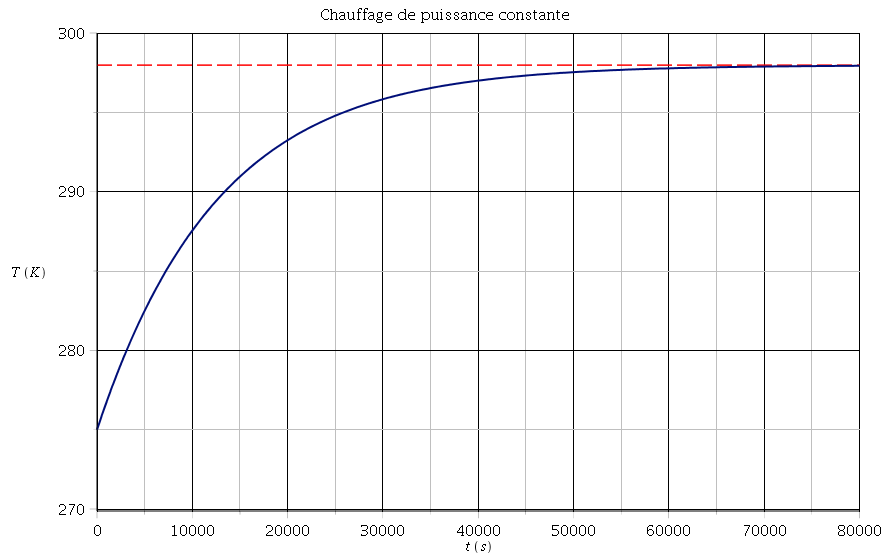
Pour la partie b), on obtient :
Je te fournis la courbe correspondante même si l'énoncé ne la demande pas. Tu pourras constater que tes valeurs numériques sont à revoir.
Merci beaucoup !
Par contre j'ai bien tout vérifié, j'obtiens toujours ces valeurs là pour t2 et t du régime permanent...
Qu'est-ce qui peut clocher ?
La valeur de a est bien celle indiquée dans ton premier message ? Si oui, la constante de temps est :
 =a-1
=a-1 1,27.104s
1,27.104s 3,52h
3,52h
Pour la question a) la durée de 3h est à peine inférieure à la constante de temps. La chute de température est nécessairement importante, pas 0,6K comme tu obtiens ! Ton résultat est totalement aberrant.
Au fait : 1h = 3600s, pas 60 ! ; je me demande si tes problèmes ne viennent pas de là !


