Inscription / Connexion Nouveau Sujet
Théorème du moment cinétique
Salut tous le monde, j'ai commencé un exercice et j'ai vu que j'avais des difficultés, pouvez vous m'aider ?
Voici l'énoncé et ce que j'ai fait:
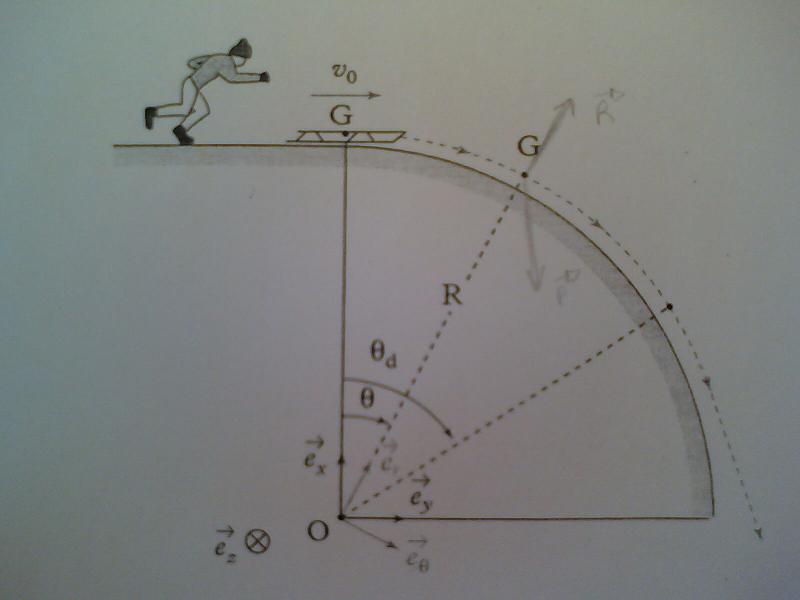
Une luge assimilée à un point matériel G de masse m arrive au niveau d'un profil circulaire avec une vitesse horizontale v0. Tant que la luge suit ce profil, elle décrit une trajectoire circulaire de rayon R=5m et est repérée par l'angle  . On néglige tous les frottements. Le réferentiel Rg (o;ex,ey,ez) lié à la Terre est supposé galiléen.
. On néglige tous les frottements. Le réferentiel Rg (o;ex,ey,ez) lié à la Terre est supposé galiléen.
1) Ecrire l'équation différentielle du mouvement à l'aide du TMC
2) En déduire l'expression de  . en fonction de la position, repérée par
. en fonction de la position, repérée par  Donner l'expression de la réaction du sol.
<br /> 4) En déduire l'angle limite [smb]theta.gif) d à partir duquel la luge quitte le profil circulaire (en fonction de v0)
d à partir duquel la luge quitte le profil circulaire (en fonction de v0)
5) Montrer qu'il existe une valeur limite de v0 au-dela de laquelle la luge ne suit pas du tout le profil circulaire. Cette valeur est elle accessible ?
Voici ce que j fait:
Bilan des forces: Poids P et Réaction R
1/(dLo(G))/(dt)= Mo(P) + Mo(R)
Mo(P)= OG  P
P
= Rmgsin .ez
.ez
Mo(R)=0
Lo(G)=OG mv(G)
mv(G)
=mR² . ez
. ez
D'où: d(mR² . ez)/dt = Rmgsin
. ez)/dt = Rmgsin ez
ez
mR² ..=Rmgsin
..=Rmgsin
 ..=g/R sin
..=g/R sin
Merci d'avance,j'espère que vous pourrez m'aider.
* Pour les questions (ya des fautes dans l'énoncés):
1) Ecrire l'équation différentielle du mouvement à l'aide du TMC
2) En déduire l'expression de  . en fonction de
. en fonction de  et de v0.
et de v0.
3) Déterminer l'expression de la réaction du sol.
4) En déduire l'angle  d à partir duquel la luge quitte le profil circulaire (en fonction de v0)
d à partir duquel la luge quitte le profil circulaire (en fonction de v0)
5) Montrer qu'il existe une valeur limite de v0 au-dela de laquelle la luge ne suit pas du tout le profil circulaire. Cette valeur est elle accessible ?
J'espère que vous pourrez m'aidez pour la suite des questions
Merci d'avance ^^
J'ai vu qu'il y a un sujet qui ressemblehttps://www.ilephysique.net/sujet-le-t-m-c-235687.html mais il y a une faute au début donc je ne comprends pas vraiment comment faire
bonsoir,
1) O" = g/R sin O
2) multiplie par O' des deux côtés et intègre la relation (sachant que d(O'2)/dt = 2 O'O" )
avec la condition initiale sur la vitesse tu trouves:
O'2 = O'o 2 + 2g(1-cos O)/R
sauf erreur
donc en fction de v0 ça fait : O'= ( (v0/R)²+ 2g(1-cos O)/R)
( (v0/R)²+ 2g(1-cos O)/R)
mais jcomprends pas d'où vient le 2 devant le "g" ... et aussi je comprends pas et je ne sais pas entre quelles bornes on intègre, vous pouvez mexpliquer ?
O" = g/R sin O
O'O" = g/R O'sin O
en intégrant:
1/2 O'2 = -g/R cos O + K
on trouve K en exprimant les conditions initiales
1)
mg.cos(theta) = m.dv/dt
dv/dt = g.sin(theta)
v = w.R
dv/dt = R.dw/dt = R.d²theta/dt²
R.d²theta/dt² = g.sin(theta)
d²theta/dt² = (g/R).sin(theta)
theta" = (g/R).sin(theta)
-----
2)
theta" = (g/R).sin(theta)
theta" * theta'= (g/R).sin(theta) . theta'
(1/2).(theta')² = -(g/R).cos(theta) + K
en theta = 0, v = Vo et w = vo/R ---> theta'(0) = Vo/R
Vo²/(2R²) = -(g/R) + K
K = Vo²/(2R²) + (g/R)
(1/2).(theta')² = -(g/R).cos(theta) + Vo²/(2R²) + (g/R)
(theta')² = -(2g/R).cos(theta) + Vo²/R² + (2g/R)
(theta')² = Vo²/R² + (2g/R).(1 - cos(theta))
theta' = Racinecarrée[Vo²/R² + (2g/R).(1 - cos(theta))]
-----
3)
N = mg.cos(theta) - m.w²R
N = mg.cos(theta) - m.R.[Vo²/R² + (2g/R).(1 - cos(theta))]
N = mg.cos(theta) - m.[Vo²/R + 2g.(1 - cos(theta))]
N = - m.[Vo²/R + g.(2 - 3.cos(theta))]
N = m.[g(3cos(theta)-2) - Vo²/R]
-----
4)
La luge quitte le profil circulaire lorsque N = 0
---> g(3cos(theta_d)-2) - Vo²/R = 0
(3cos(theta_d)-2) = Vo²/(R.g)
3cos(theta_d) = 2 - Vo²/(R.g)
cos(theta_d) = (2 - Vo²/(R.g))/3
theta_d = arccos[(2 - Vo²/(R.g))/3]
-----
5)
Si on calcule N <= 0 pour theta = 0, alors la luge ne suit pas du tout le profil circulaire.
Soit donc si : g(3cos(0)-2) - Vo²/R <= 0
Vo²/R >= g
Vo² >= g.R
Vo >= racinecarrée[g.R]
Donc la valeur limite de v0 au-dela de laquelle la luge ne suit pas du tout le profil circulaire est Vo = racinecarrée[g.R]
-----
Aucun calcul vérifié.
Recopier sans comprendre est inutile.



