Inscription / Connexion Nouveau Sujet
Theorème de stokes
Bonsoir,
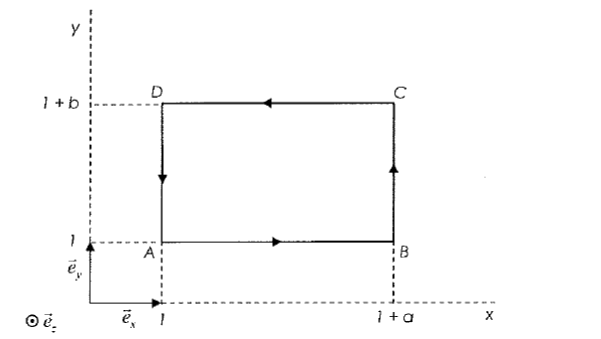
Je bloque sur un exercice, on me demande de vérifier le théorème de stokes sur ce contour :
On nous donne A=y(ex)+z(ey)+x(ez)
Donc je calcule integrale(A.dl) en la découpant en pleureuses intégrales
On me demande de calculer I1=l'intégrale(A.dl) sur la longueur AB en fonction de a , je trouve I1=ay (je dois avoir une erreur on doit trouver que en fonction de a )
On me demande de calculer I2=l'intégrale(Adl) sur la longueur BC en fonction de Z et b : je trouve I2=bz
On me demande de calculer I3=l'intégrale(A.dl) sur la longueur CD en fonction de a et b , ici je ne vois pas comment faire
On me demande de calculer I4=l'intégrale(A.dl) sur la longueur DA en fonction de z et b : je trouve I4=bz
Pouvez vous m'aider?
Merci d'avance
Bonsoir à tous les deux,
rien que pour le gag des intégrales pleureuses qui m'a fait sourire, voici le calcul :
I - circulation de A :
a) le long de AB :
dl = dx.
donc A.dl = y.dx = dx puisque tous les points du segment AB ont pour ordonnée y = 1. L'abscisse x du point courant varie de 1 à 1+a. Donc cette première circulation vaut I1 = a.
b) Le long de BC :
dl = dy.
donc A.dl = z.dy =0 puis que z est constamment nul. I2 = 0.
c) De C vers D :
un conseil que l'on m'a donné quand j'étais en classe prépa (pas d'hier...) : Calculons plutôt la circulation de D vers C et ajoutons le signe - à la fin du calcul. OK ?
Sur le segment CD, A.dl = y.dx (comme pour I1), où y = 1+b et x varie de 1 à 1+a. On obtient la circulation de D vers C égale à a(1 + b), soit I3 = -a(1 + b).
d) de D vers A :
A.dl = -z.dy = 0 à cause de z, soit I4 = 0.
Bilan : I1 + I2 + I3 + I4 = -ab
II - flux du rotationnel de A à travers toute surface s'appuyant sur le contour fermé ABCDA :
Avec les formules classiques donnant les composantes du rotationnel de A : rotA = - - - 
.
La surface la plus simple s'appuyant sur le contour est évidemment la surface du rectangle ABCD. Le sens de parcours choisi pour la circulation (A
BCDA) impose d'orienter l'unitaire de cette surface comme l'unitaire de l'axe Oz.
Du coup, rotA.n.ds = -ds, et le flux de rotA vaut bien -ab. : Th. vérifié !
Annuler
connectez vous