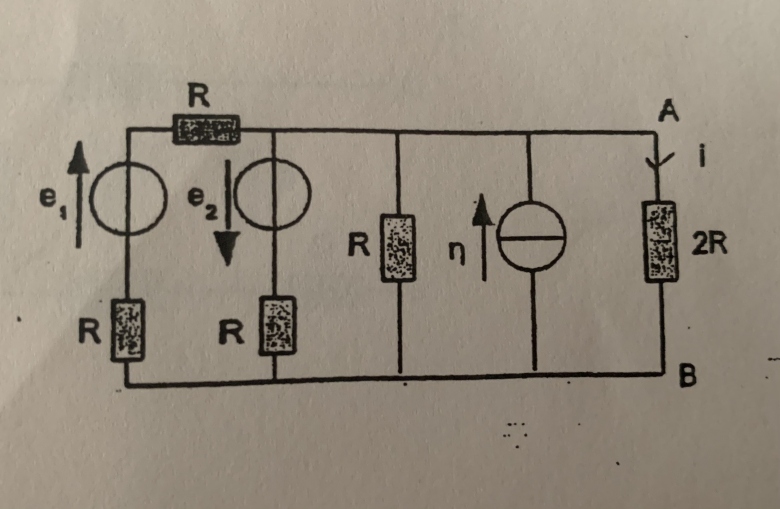
au final je trouve i = /6-e₂/6R +e₁/6
et en faisant plusieurs equivalences thevenin - norton pour me ramener a une seule maille je trouve  i = /4-e₂/4R +e₁/4
mais vu que les deux expressions sont proportionnele j'imagine que j'ai juste commis une erreur de calcul dans la seconde methode

Bonsoir
Le théorème de Millman n'est que la loi des neouds dans laquelle ont remplace aussitôt les intensités par leurs expressions déduites de la loi d'Ohm sauf les intensités produites par les générateurs de courant que l'on conserve.

J'ai eu l'occasion d'expliquer cela en détail sur la fiche ci-dessous :

bonsoir
en effet en le voyant comme la loi des nœuds , je vois bien que je ne dois pas m'arrêter au premier nœud devant A car je dois faire la somme des courants venants de toutes les branches
merci a vous

En tenant compte de ces remarques, qu'obtiens-tu comme résultat ?

en appliquant le theoreme de millman en A , en prenant B comme masse et en utilisant Va-Vb  = 2Ri
j'obtiens  i = /6-e2/6R +e1/6

Ton résultat est nécessairement faux car il n'est pas homogène. Une intensité ne peut apparaître que comme une somme algébrique de termes ayant la dimension physique d'une intensité. C'est le cas de   et de e2/6R mais pas le cas de e1/6 qui a la dimension d'une tension.



Je te laisse simplifier puis appliquer la loi d'Ohm à la résistance « 2R » entre A et B.

N'hésite pas à poser des questions si tu ne comprends pas bien l'application du théorème de Millman.

bonjour
après simplification j'obtiens i  =i = /6-e2/6R +e1/12R qui a bien les bonnes dimensions , sinon j'avais une autre question sur l'application du théorème de millman que fait t on lorsque une branche contient un generateur idéal de courant en serie avec une resistance , en effet je sais qu'on peut modeliser un generateur reel soit avec le modele de norton soit celui de thevenin mais pour un un generateur ideal de courant en serie avec une resistance j'ai un peu de mal a le comprendre ?
merci

Imagine que tu ajoutes une résistance en série dans la branche  du générateur idéal de courant. Cela ne modifierait en rien la tension U_AB et donc l'intensité I demandé. Un générateur idéal de courant fournit dans sa branche une intensité bien précise et cela quelle que soit la tension à ses bornes.
Cette remarque est importante : lorsque l'on cherche à modéliser un circuit, on peut commencer par remplacer par de simples fils conducteurs de résistance négligeable tous les dipôles présents dans la branche d'un générateur idéal de courant, en conservant bien sûr le générateur idéal de courant.

bonjour
les choses sont plus claires pour moi désormais grâce a vos explications.
merci à vous