Niveau licence

Theoreme de Guldin appliqué à une fibre neutre

Posté par
tcheips 17-12-09 à 08:51

Bonjour,

J'ai un cours d'emboutissage dans lequel on étudie les fibres neutre de pieces embouties.
On à vu la formule de guldin qui dit ceci :

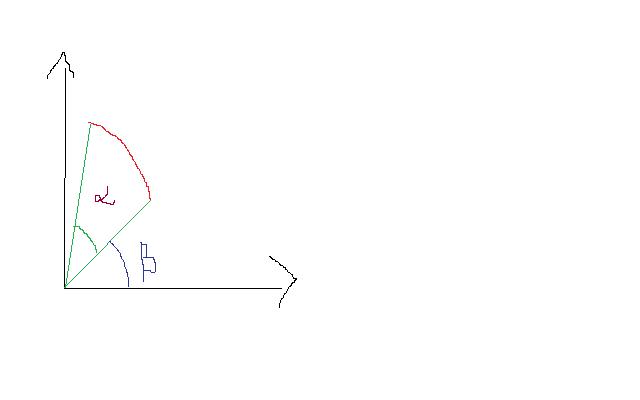
Soit O le centre d'un arc de cercle G son centre de gravité.

OG = R/ (sin()_sin+) selon l'axe x

La deusieme partie du theoreme concernent l'axe y mais elle ne mais pa utile.

Mon probleme et que je n'arrive pas toujours a determiner les angles et.
Je sait que et l'angle de courbure de l'arc de cercle mais je ne sait pas trouver .

Mon but étant de calculer la distance entre le centre géometrique et le centre de gravité d'un arc de cercle. (pour un demi cercle ils sont les memes). Mais pour un autre type d'angle?...

Ci joint le shémas de mon theoreme et un exemple de shémas d'exam .

Je n'ai rien trouver sur le net donc je me tourne vers vous.

Theoreme de Guldin appliqué à une fibre neutre

Posté par centre de gravité d'un arc de cercle 17-12-09 à 10:53

Bonjour,

J'aurais voulu savoir si vous pouviez m'indiquer la marche a suivre pour calculé la distance entre le centre géométrique et le centre de gravité d'un arc de cercle quelconque?

Merci d'avance.

*** message déplacé ***

Posté par re : Theoreme de Guldin appliqué à une fibre neutre 17-12-09 à 14:58

Que cherches-tu à faire exactement?

Déterminer les valeurs de $\alpha$ et $\beta$ pour les arcs de cercle figurant sur tes schémas?

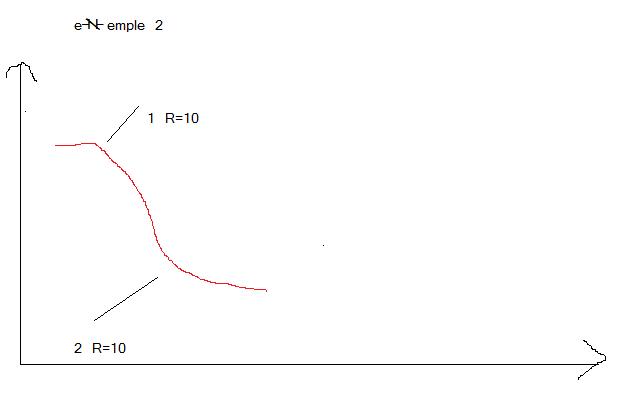
Posté par re : Theoreme de Guldin appliqué à une fibre neutre 17-12-09 à 15:30

Oui surtout pour l'exemple 2 l'autre je sais le faire.

Posté par re : Theoreme de Guldin appliqué à une fibre neutre 17-12-09 à 21:53

Le deuxième exemple est compliqué parce que même avec de la bonne volonté je ne vois pas d'arcs de cercle...

Mais de façon générale, la marche à suivre consiste à placer un repère au niveau du centre géométrique, comme sur le schéma servant à établir la formule générale. Il ne te reste plus qu'à comparer pour déterminer $\beta$ et $\alpha$ ... $\alpha$ est lié la longueur de l'arc, $\beta$ à sa position (angulaire) par rapport à l'axe horizontal.

Posté par re : Theoreme de Guldin appliqué à une fibre neutre 18-12-09 à 10:05

Merci donaldos,

Justement je bloque sur la position angulaire par rapport a l'axe horizontale.
Euuuu sa signifie quoi éxactement ?

Posté par re : Theoreme de Guldin appliqué à une fibre neutre 18-12-09 à 12:52

On te donne un arc de cercle.

Représente-toi le cercle complet. On repère un point de ce cercle par l'angle $\theta$ mesuré à partir de l'axe $(O, \vec{x})$ .

L'arc de cercle est défini comme l'ensemble des points du cercle correspondant à $\theta \in [\beta,\beta+\alpha]$ , non?

Si l'on parcourt l'arc de cercle dans le sens trigonométrique, le point correspondant à l'angle $\beta$ est donc le point de départ, la première extrémité de l'arc de cercle. C'est représenté de façon on ne peut plus claire sur ton tout premier schéma!

Tu repères donc ce point pour chaque arc de cercle et tu mesures l'angle formé avec l'axe $(0,\vec{x})$ et tu as $\beta$ ... La lecture est immédiate.

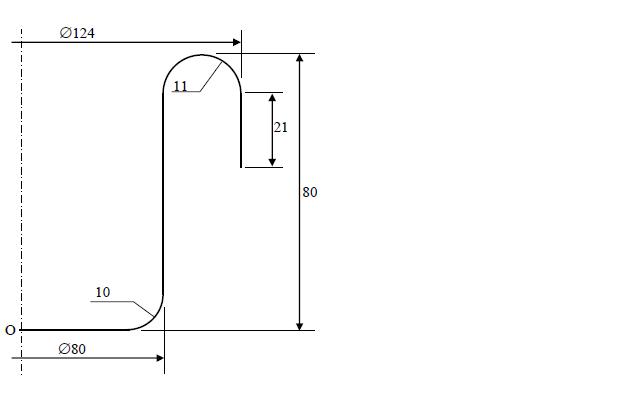
Pour ton premier schéma on a ainsi :

-pour l'arc de cercle de rayon 10 : $\beta=-\pi/2$ , $\alpha=\pi/2$

-pour l'arc de cercle de rayon 11: $\beta=0$ , $\alpha = \pi$

Si tu ne vois pas ça, je ne pense pas pouvoir t'aider...