Bonsoir,
J'ai de nouveau un exercice avec la correction mais je ne la comprend pas car elle n'est pas beaucoup détailler donc j'ai besoin d'aide !

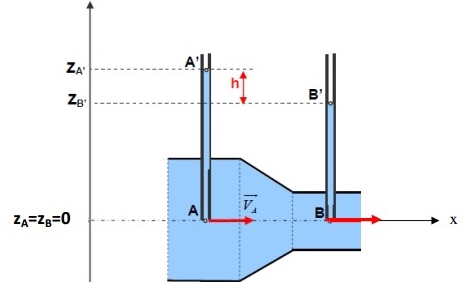
Une conduite de section principale S_A, de diamètre d, subit un étranglement en B où sa section est
S_B. On désigne par = S_A/S_B le rapport des sections.
Un fluide parfait incompressible de masse volumique , s'écoule à l'intérieur de cette conduite.
L'écoulement dans la conduite est uniforme par tranche et quasi-stationnaire.
Deux tubes plongent dans la conduite ayant des extrémités respectivement A et B. Les extrémités libres des deux tubes sont à la pression atmosphérique P_atm.
Par lecture directe de la dénivellation h, les deux tubes permettent de mesurer le débit volumique q_v qui traverse la conduite.

1) Déterminer les pressions en A et en B en fonction de (P_atm, z_A', z_B', )

Pour ça c'est bon j'ai compris j'ai :
P_A = P_atm + gz_A'
P_B + p_ATM + GZ_B'

2) Établir, en la justifiant, une relation entre les vitesses d'écoulement V_A en A et V_B en B.
Pour ça j'ai également compris :
Conservation du débit : S_AV_A = S_BV_B ⇒ V_B = V_A

3) Déterminer la différence de pression (P_B-P_A) en fonction de V_A, , et .

Je ne comprend par d'ou sors la formule de Bernouilli et comment ils l'applique !
On peur appliquer ici le théorème de Bernouilli entre A et B :
P_A + gz_A + 1/2 * V_A² = P_B + gz_B + 1/2 * V_B²
avec z_A = z_B
d'où
P_B - P_A = 1/2 * (V_A² - V_B²) = 1/2 * V_A²(1-²)


Merci par avance